Алгебра
2024
В системе двух уравнений с двумя переменными первым является уравнение \(y-|x|=0\), а вторым уравнение вида \(y=k x+b\), где \(k\) и \(b\) - некоторые числа. Известно, что прямая - график второго уравнения пересекает ось \(x\) в точке \((-3; 0)\). Подберите в уравнении \(y=k x+b\) коэффициенты \(k\) и \(b\) так, чтобы система:
1) имела два решения;
2) имела одно решение;
3 ) не имела решений.
Начнем с системы уравнений:
\(\begin{cases}y - |x| = 0 \\y = kx + b\end{cases}\) и переходим к: \(\begin{cases}y = |x| \\y = kx + b\end{cases}\)
Подставляя \((-3, 0)\) в уравнение \(y = kx + b\), получим \(0 = -3k + b\), что ведет к \(b = 3k\).
Далее, рассмотрим различные случаи в зависимости от значений \(k\) и \(b\):
•
Два решения: \(k = \frac{1}{3}\) и \(b = 3k = 1\), что дает уравнение \(y = \frac{x}{3} + 1\).
•
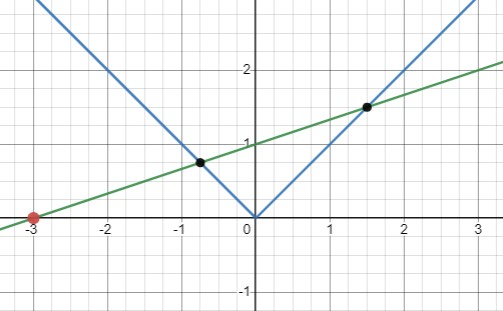
Одно решение: \(k = 1\) и \(b = 3k = 3\), что дает уравнение \(y = x + 3\).
•
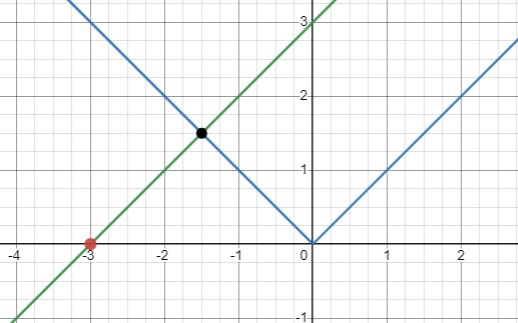
Нет решений: \(k = -1\) и \(b = 3k = -3\), что дает уравнение \(y = -x - 3\).
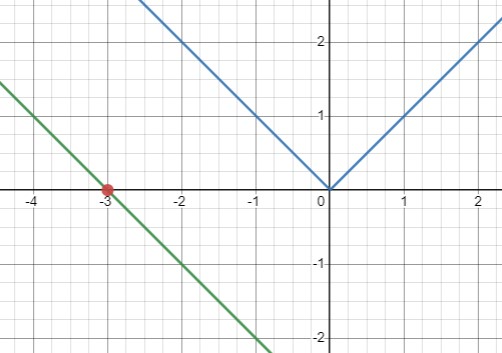
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
В системе двух уравнений с двумя переменными первым является уравнение \(y-|x|=0\), а вторым уравнение вида \(y=k x+b\), где \(k\) и \(b\) - некоторые числа. Известно, что прямая - график второго уравнения пересекает ось \(x\) в точке \((-3; 0)\). Подберите в уравнении \(y=k x+b\) коэффициенты \(k\) и \(b\) так, чтобы система: 1) имела два решения; 2) имела одно решение; 3 ) не имела решений.
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
