Вертикаль
2018
Изобразив схематически графики уравнений, выясните, имеет ли решения система уравнений и если имеет, то сколько:
а) \(\begin{cases}y=x^{3} \\ x y=-12\end{cases}\)
б) \(\begin{cases}y=x^{2}+8 \\ y=-x^{2}+12\end{cases}\)
в) \(\begin{cases}y=x^{2}+1, \\ x y=3\end{cases}\)
а
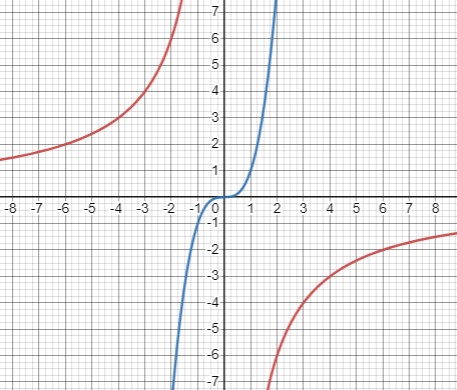
\(\begin{cases}y = x^3 \\xy = -12\end{cases}\) приводит к уравнениям: \(\begin{cases}y = x^3 \\y = -\frac{12}{x}\end{cases}\)
Они не пересекаются, следовательно, у системы нет решений.
б
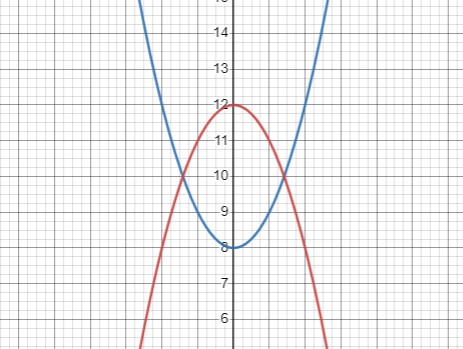
Cистема уравнений: \(\begin{cases} y = x^2 + 8 \\y = -x^2 + 12\end{cases}\)
имеет два уравнения, каждое из которых задает параболу.
Решение состоит из точек пересечения этих двух парабол: это две точки, так как уравнения парабол имеют два решения.
в
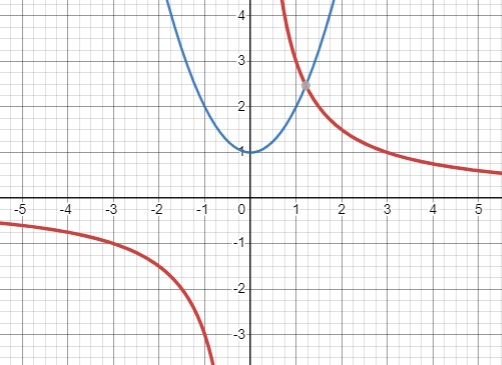
Система уравнений: \(\begin{cases}y = x^2 + 1 \\xy = 3\end{cases}\) приводит к уравнениям: \(\begin{cases} y = x^2 + 1 \\y = \frac{3}{x}\end{cases}\)
Теперь мы имеем одно уравнение квадратичной параболы и одно уравнение гиперболы. У системы будет одна общая точка пересечения этих двух кривых.
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Изобразив схематически графики уравнений, выясните, имеет ли решения система уравнений и если имеет, то сколько: а) \(\begin{cases}y=x^{3} \\ x y=-12\end{cases}\) б) \(\begin{cases}y=x^{2}+8 \\ y=-x^{2}+12\end{cases}\) в) \(\begin{cases}y=x^{2}+1, \\ x y=3\end{cases}\)
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
