§ 10. Уравнения с двумя переменными и их системы — 31. Алгебраический способ решения систем уравнений — 709 — стр. 168

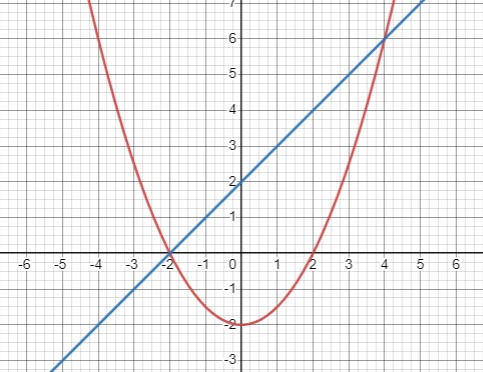
Графический способ:

Уравнения системы:

\(y = 0.5x^2 - 2\)

\(y - x = 2\)

Первое уравнение описывает параболу с вершиной в точке \((0, -2)\), осью симметрии \(x = 0\), и пересекает ось \(y\) в точке \((0, -2)\).

Второе уравнение описывает прямую с коэффициентом наклона 1 и точкой пересечения с осью \(y\) в \((0, 2)\).

Графическое решение: \((-2, 0)\) и \((4, 6)\).

Аналитический способ:

Мы преобразуем систему уравнений:

\(\begin{cases}y = 0.5x^2 - 2 \\y - x = 2\end{cases} \Leftrightarrow\begin{cases}x + 2 = 0.5x^2 - 2 \\y = x + 2\end{cases} \Leftrightarrow\)

\( \Leftrightarrow \begin{cases}0.5x^2 - x - 4 = 0 \\y = x + 2\end{cases} \Leftrightarrow \begin{cases}x^2 - 2x - 8 = 0 \\y = x + 2\end{cases} \Leftrightarrow \)

\(\Leftrightarrow\begin{cases}(x + 2)(x - 4) = 0\\y = x + 2\end{cases} \Leftrightarrow\begin{cases}\begin{cases}x = -2 \\x = 4 \end{cases}\\y = x + 2\end{cases}\Leftrightarrow\begin{cases}\begin{cases}x = -2 \\y = -2+2=0 \end{cases}\\\begin{cases}x=4\\y = 4 + 2=6\end{cases}\end{cases}\)

Решение аналитически: \((-2, 0)\) и \((4, 6)\).