Алгебра
2024
Проиллюстрируйте с помощью кругов Эйлера соотношение между множеством \(\boldsymbol{N}\) натуральных чисел, множеством \(\boldsymbol{Z}\) целых чисел, множеством \(Q\) рациональных чисел. Найдите пересечение и объединение:
a) множества натуральных и множества целых чисел;
б) множества целых и множества рациональных чисел;
в) множества рациональных и множества иррациональных чисел.
а
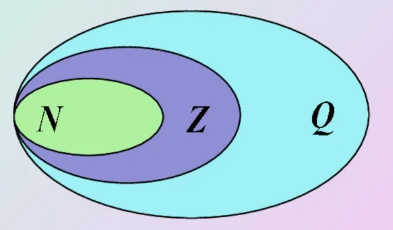
\(\mathrm{N} \cap \mathrm{Z}=\mathrm{N} ; \mathrm{N} \cup \mathrm{Z}=\mathrm{Z}\).
б
\(\mathrm{Z} \cap \mathrm{Q}=\mathrm{Z} ; \mathrm{Z} \cup \mathrm{Q}=\mathrm{Q}\).
в
\(\mathrm{Q} \cap \mathrm{I}=\emptyset ; \mathrm{Q} \cup \mathrm{I}=\mathrm{R}\).
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Проиллюстрируйте с помощью кругов Эйлера соотношение между множеством \(\boldsymbol{N}\) натуральных чисел, множеством \(\boldsymbol{Z}\) целых чисел, множеством \(Q\) рациональных чисел. Найдите пересечение и объединение: a) множества натуральных и множества целых чисел; б) множества целых и множества рациональных чисел; в) множества рациональных и множества иррациональных чисел.
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
