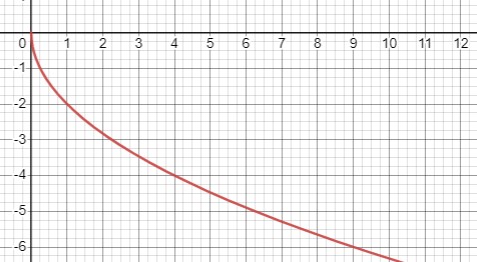
Постройте график функции \(f(x)=-2 \sqrt{x}\). Как изменяются значения данной функции с увеличением значений аргумента от 0 до \(+\infty\) (увеличиваются или уменьшаются)? Укажите область определения и множество значений данной функции.
У нас дана функция \( f(x) = -2 \sqrt{x} \).
Так как коэффициент перед корнем отрицательный (\( -2 \)), функция будет убывающей. Это означает, что при увеличении значения аргумента \( x \), значение функции \( f(x) \) будет уменьшаться.
Теперь определим область определения и область значений функции:
Область определения: так как подкоренное выражение \( x \) должно быть неотрицательным, то \( D(y) = [0 ; +\infty) \), то есть все неотрицательные действительные числа.
Область значений: учитывая знак минус перед корнем, функция принимает отрицательные значения. Таким образом, \( E(y) = (-\infty ; 0] \).
Итак, мы получаем:
Область определения: \( (0 ; +\infty) \)
Область значений: \( (-\infty ; 0) \)
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Постройте график функции \(f(x)=-2 \sqrt{x}\). Как изменяются значения данной функции с увеличением значений аргумента от 0 до \(+\infty\) (увеличиваются или уменьшаются)? Укажите область определения и множество значений данной функции.

