§ 16. Стандартный вид числа — 51. Функции и их свойства — 1245 — стр. 278

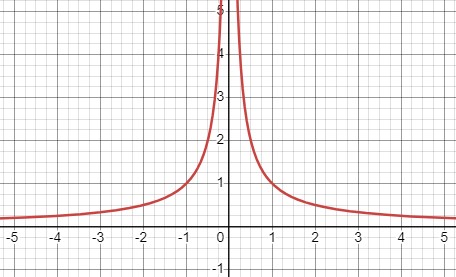
Давайте разберемся с данной функцией по шагам.

У нас есть функция \(y = |x^{-1}| = |\frac{1}{|x|}\), которая определяется следующим образом:
\(y = \begin{cases}\frac{1}{x}, & \text{если } x > 0 \\-\frac{1}{x}, & \text{если } x < 0\end{cases}\)

Таким образом, график данной функции симметричен относительно оси \(x\).

Это означает, что если мы возьмем точку \((x, y)\), то симметричная ей точка будет иметь координаты \((-x, y)\).