Постройте в одной системе координат графики функций \(y=x^{-1}\), где \(x>0\), и \(y=x^{-2}\), где \(x>0\). Сравните значения \(x^{-1}\) и \(x^{-2}\), если:
a) \(0<x<1\);
б) \(x>1\).
\(y = x^{-1}\), где \(x > 0\).
\(y = x^{-2}\), где \(x > 0\).
а
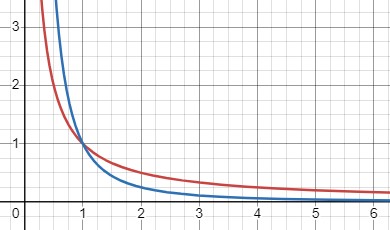
При \(0 < x < 1\):
Для \(x^{-1}\) значение уменьшается при увеличении \(x\) (так как \(x\) в знаменателе), следовательно, \(x^{-1} < x^{-2}\) при \(0 < x < 1\).
б
При \(x > 1\):
Для \(x^{-1}\) значение уменьшается при увеличении \(x\), в то время как для \(x^{-2}\) значение увеличивается (так как \(x\) в знаменателе возводится во вторую степень), следовательно, \(x^{-1} > x^{-2}\) при \(x > 1\).
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Постройте в одной системе координат графики функций \(y=x^{-1}\), где \(x>0\), и \(y=x^{-2}\), где \(x>0\). Сравните значения \(x^{-1}\) и \(x^{-2}\), если: a) \(0<x<1\); б) \(x>1\).
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
