Вертикаль
2016
(Для работы в парах.) Решите графически уравнение:
а) \(x^{2}-2 x-1=0\);
б) \(x^{2}-4 x+2=0\).
1) Обсудите друг с другом, в каком виде удобно представить уравнение.
2) Распределите, кто выполняет задание а), а кто - задание б), и выполните их.
3) Найдите корни каждого из уравнений с помощью формулы корней квадратного уравнения и сравните их со значениями, найденными при графическом решении.
а
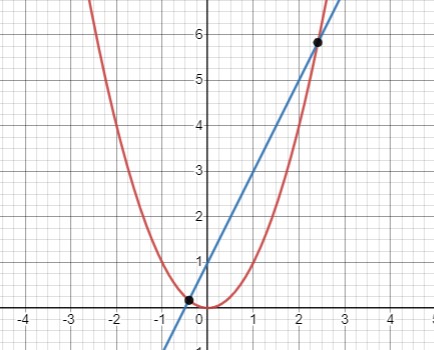
Уравнение \(x^2 - 2x - 1 = 0:\)
Графическое решение: Пересечения графика с осью абсцисс: \(x_1 \approx -0.41\), \(x_2 \approx 2.41\).
Аналитическое решение: Вычисляем дискриминант: \(D = 1^2 - 1 \cdot (-1) = 2\). Находим корни: \(x = 1 \pm \sqrt{2}\).
б
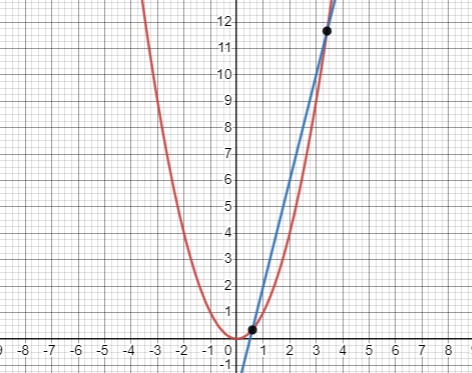
Уравнение \(x^2 - 4x + 2 = 0:\)
Графическое решение: Пересечения графика с осью абсцисс: \(x_1 \approx 0.59\), \(x_2 \approx 3.41\).
Аналитическое решение: Вычисляем дискриминант: \(D = 2^2 - 1 \cdot 2 = 2\). Находим корни: \(x = 2 \pm \sqrt{2}\).
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
(Для работы в парах.) Решите графически уравнение: а) \(x^{2}-2 x-1=0\); б) \(x^{2}-4 x+2=0\). 1) Обсудите друг с другом, в каком виде удобно представить уравнение. 2) Распределите, кто выполняет задание а), а кто - задание б), и выполните их. 3) Найдите корни каждого из уравнений с помощью формулы корней квадратного уравнения и сравните их со значениями, найденными при графическом решении.
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
