С помощью графиков выясните, сколько корней может иметь уравнение \(\frac{1}{x}=a x+b\), где \(a\) и \(b-\) некоторые числа. Для каждого случая укажите, каким условиям должны удовлетворять числа \(a\) и \(b\).
При \(a>0, b>0\) - два корня
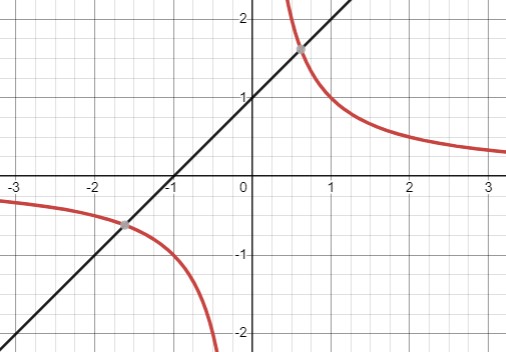
При \(a>0, b<0\) - два корня

При \(a<0, -2<b<2\) - нет корней
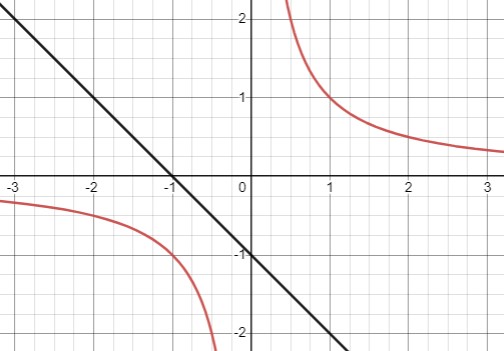
При \(а<0, b=\pm2\) - два корня
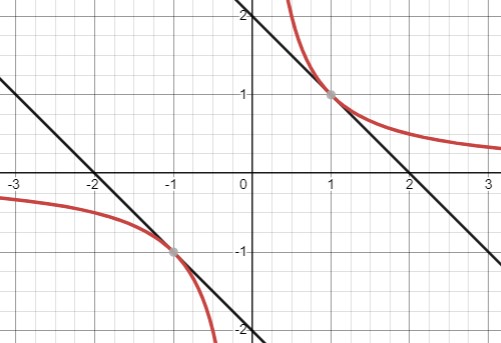
При \(a<0,b<-2,b>2\) - два корня
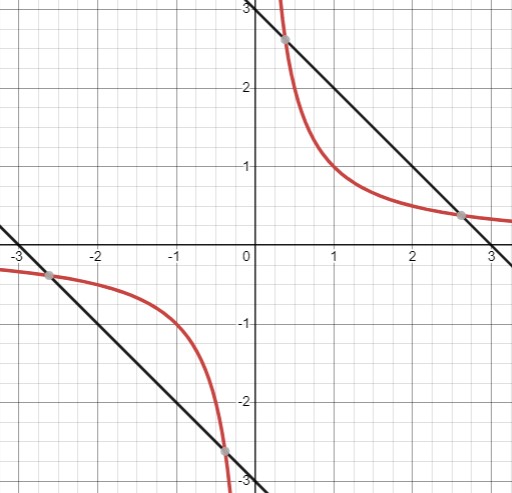
При \(a=0,b<0\) - один корень
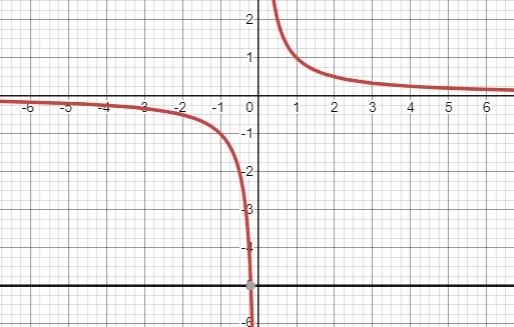
При \(a=0,b>0\) - один корень
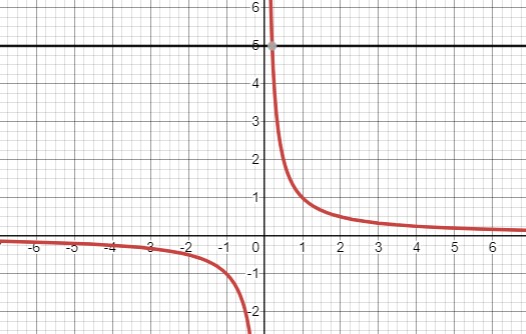
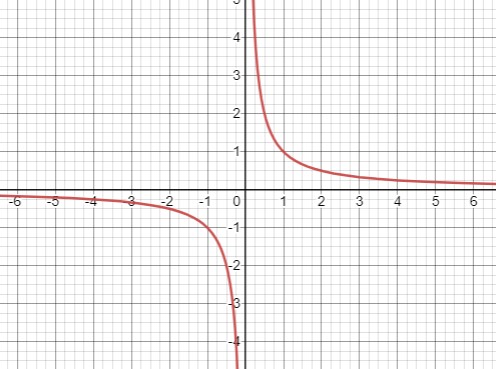
При \(a=0,b=0\) - нет корней
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
С помощью графиков выясните, сколько корней может иметь уравнение \(\frac{1}{x}=a x+b\), где \(a\) и \(b-\) некоторые числа. Для каждого случая укажите, каким условиям должны удовлетворять числа \(a\) и \(b\).

