Найдите область определения функции и постройте ее график:
a) \(y=\frac{36}{(x+1)^{2}-(x-1)^{2}}\);
б) \(y=\frac{18-12 x}{x^{2}-3 x}-\frac{6}{3-x}\);
в) \(y=\frac{16}{(2-x)^{2}-(2+x)^{2}}\);
г) \(y=\frac{3 x(x+1)-3 x^{2}+15}{x(x+5)}\).
а
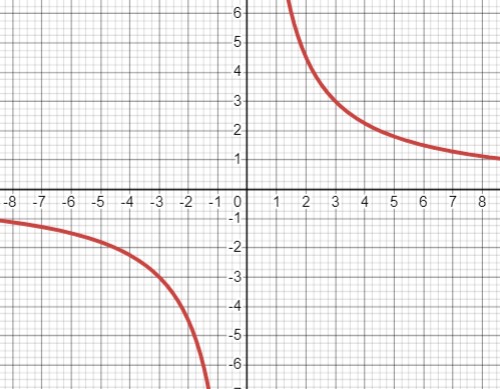
Исходное уравнение:
- \(y=\frac{36}{(x+1)^2-(x-1)^2}\).
- Ограничения на переменную \(x\):
- \((x+1)^2-(x-1)^2 \neq 0\).
- Решение: \(x \neq 0\).
- Область определения:
- \(x \in (-\infty ; 0) \cup (0 ; +\infty)\).
- Преобразования уравнения:
- Функция \(y=\frac{36}{4 x}=\frac{9}{x}\) - обратная пропорциональность.
- Особая точка \(x \neq 0\) сохраняется при преобразованиях.
- Таким образом, \(y=\frac{36}{(x+1)^2-(x-1)^2} \Leftrightarrow y=\frac{9}{x}\).
б
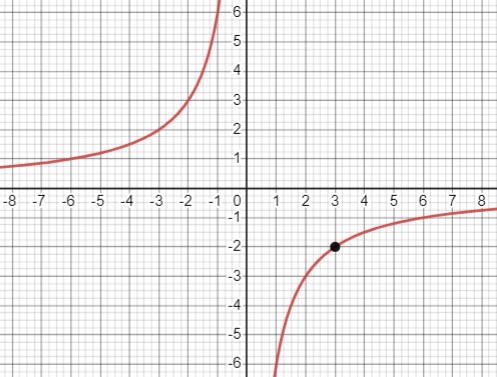
Исходное уравнение:
- \(y=\frac{18-12 x}{x^2-3 x}-\frac{6}{3-x}\).
- Ограничения на переменную \(x\):
- \(x^2-3 x \neq 0\).
- \(3-x \neq 0\).
- Решение: \(x \neq \{0 ; 3\}\).
- Область определения:
- \(x \in (-\infty ; 0) \cup (0 ; 3) \cup (3 ; +\infty)\).
- Преобразования уравнения:
- Функция \(\frac{18-12 x}{x^2-3 x}-\frac{6}{3-x}=-\frac{6}{x}\).
- Особая точка \(x \neq 0\) сохраняется при преобразованиях.
- Особую точку \(x \neq 3\) необходимо учесть дополнительно.
- Таким образом, \(y=\frac{18-12 x}{x^2-3 x}-\frac{6}{3-x} \Leftrightarrow \left\{\begin{array}{c} y=-\frac{6}{x} \\ x \neq 3 \end{array}\right.\).
в
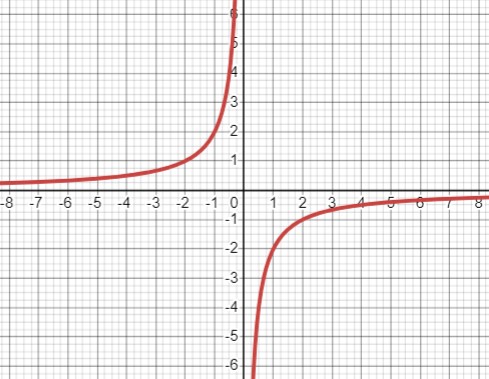
Исходное уравнение:
- \(y=\frac{16}{(2-x)^2-(2+x)^2}\).
- Ограничения на переменную \(x\):
- \((2-x)^2-(2+x)^2 \neq 0\).
- Решение: \(x \neq 0\).
- Область определения:
- \(x \in (-\infty ; 0) \cup (0 ; +\infty)\).
- Преобразования уравнения:
- Функция \(y=\frac{16}{-8 x}=-\frac{2}{x}\).
- Особая точка \(x \neq 0\) сохраняется при преобразованиях.
- Таким образом, \(y=\frac{16}{(2-x)^2-(2+x)^2} \Leftrightarrow y=-\frac{2}{x}\).
г
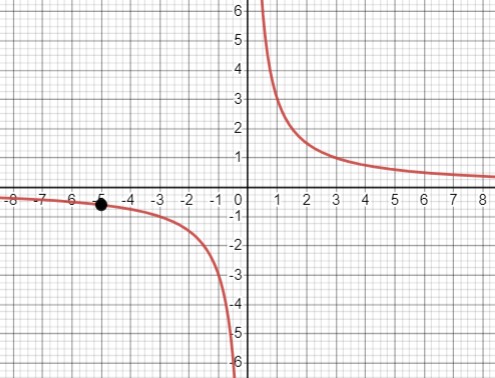
Исходное уравнение:
- \(y=\frac{3 x(x+1)-3 x^2+15}{x(x+5)}\).
- Ограничения на переменную \(x\):
- \(x(x+5) \neq 0\).
- Решение: \(x \neq \{-5 ; 0\}\).
- Область определения:
- \(x \in (-\infty ; -5) \cup (-5 ; 0) \cup (0 ; +\infty)\).
- Преобразования уравнения:
- Функция \(\frac{3 x(x+1)-3 x^2+15}{x(x+5)}=\frac{3(x+5)}{x(x+5)}=\frac{3}{x}\).
- Особая точка \(x \neq 0\) сохраняется при преобразованиях.
- Особую точку \(x \neq -5\) необходимо учесть дополнительно.
- Таким образом, \(y=\frac{3 x(x+1)-3 x^2+15}{x(x+5)} \Leftrightarrow \left\{\begin{array}{c} y=\frac{3}{x} \\ x \neq -5 \end{array}\right.\).
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Найдите область определения функции и постройте ее график: a) \(y=\frac{36}{(x+1)^{2}-(x-1)^{2}}\); б) \(y=\frac{18-12 x}{x^{2}-3 x}-\frac{6}{3-x}\); в) \(y=\frac{16}{(2-x)^{2}-(2+x)^{2}}\); г) \(y=\frac{3 x(x+1)-3 x^{2}+15}{x(x+5)}\).
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
