Дополнительные упражнения к главе I — К параграфу 3 — 261 — стр. 62

Для начала, давайте разберемся с данным уравнением:
\(y=-4-\frac{x+2}{x^{2}+2 x}=-4-\frac{x+2}{x(x+2)}=-4-\frac{1}{x}, \quad x \neq-2 \)
\(\begin{cases}y=-\frac{1}{x}-4 \\x \neq-2\end{cases}\)
Мы видим, что данное уравнение может быть переписано в виде: \(y = -\frac{1}{x} - 4\), с условием \(x \neq -2\). Это позволяет нам провести некоторые выводы о его поведении.

Построим график \(y = -\frac{1}{x} - 4\). Это график \(y = -\frac{1}{x}\), опущенный на 4 единицы вниз.

Точка \((-2, -3.5)\) не принадлежит к графику, так как она не определена для \(x = -2\).

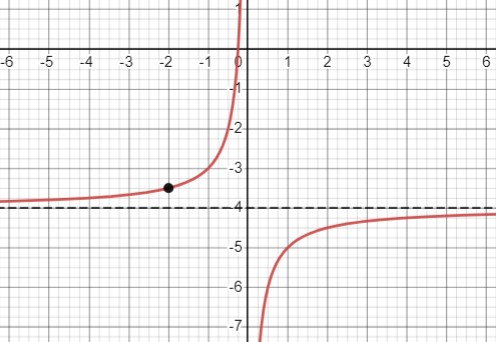
Что касается асимптоты \(y = -4\), она параллельна оси \(x\) и находится на расстоянии 4 единицы ниже оси \(x\). Нет общих точек между графиком \(y = -\frac{1}{x} - 4\) и асимптотой \(y = -4\), так как асимптота не пересекает график.

Таким образом, у нас есть график функции \(y = -\frac{1}{x} - 4\), который представляет собой гиперболу, смещенную вниз на 4 единицы, и не имеющую общих точек с асимптотой \(y = -4\).