Дополнительные упражнения к главе I — К параграфу 3 — 263 — стр. 62

\(y=\frac{|2 x-18|}{x-9}=\frac{2|x-9|}{x-9}=\begin{cases}-2, \quad x<0 \\2, \quad x \geq 0\end{cases}, \quad x \neq 9\)

1. Начнем с уравнения \(y=\frac{|2x-18|}{x-9}\).

2. Мы видим, что \(|2x - 18|\) эквивалентно \(2|x - 9|\), так как \(|a - b| = |b - a|\).

3. Заметим, что \(x - 9\) в знаменателе приводит к условию \(x \neq 9\), чтобы избежать деления на ноль.

4. Для \(x < 0\), \(x - 9 < 0\), следовательно, \(|x - 9| = -(x - 9) = 9 - x\). Значит, \(y = \frac{2(9 - x)}{x - 9} = -2\).

5. Для \(x \geq 0\), \(x - 9 \geq 0\), поэтому \(|x - 9| = x - 9\). Таким образом, \(y = \frac{2(x - 9)}{x - 9} = 2\).

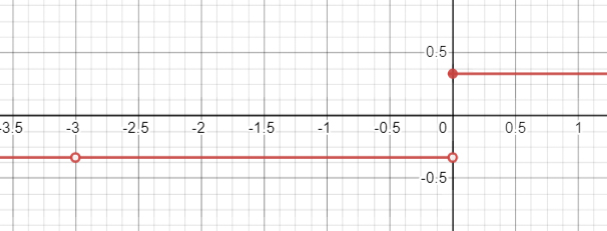
\(y=\frac{|x+3|}{3 x+9}=\frac{|x+3|}{3(x+3)}=\begin{cases}-\frac{1}{3}, \quad x<0 \\\frac{1}{3}, \quad x \geq 0\end{cases}, \quad x \neq-3\)

1. Рассмотрим уравнение \(y=\frac{|x+3|}{3 x+9}\).

2. \(|x + 3|\) эквивалентно \(|-(x + 3)| = |x + 3|\).

3. \(3x + 9 = 3(x + 3)\).

4. Условие \(x \neq -3\) нужно, чтобы избежать деления на ноль.

5. Для \(x < 0\), \(3x + 9 < 0\), а \(|x + 3| = -(x + 3)\). Таким образом, \(y = \frac{-(x + 3)}{3(x + 3)} = -\frac{1}{3}\).

6. Для \(x \geq 0\), \(3x + 9 \geq 0\) и \(|x + 3| = x + 3\). Тогда \(y = \frac{x + 3}{3(x + 3)} = \frac{1}{3}\).