Физика
2023
При каких значениях \(k\) и \(b\) гипербола \(y=\frac{k}{x}\) и прямая \(y=k x+b\) проходят через точку:
a) \(P(2 ; 1)\);
б) \(Q(-2 ; 3)\);
в) \(R(-1 ; 1)\)?
а
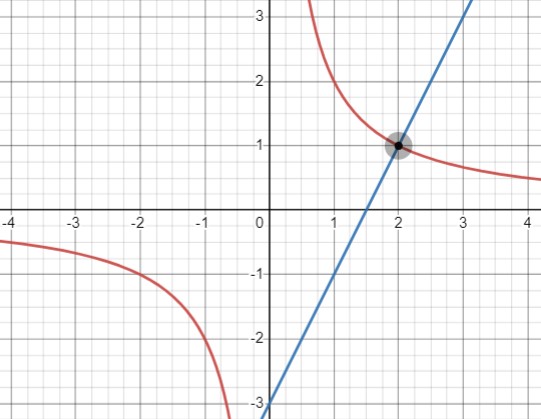
Для точки \( P \) с координатами \( (2, 1) \), мы находим произведение \( k = x \cdot y = 2 \cdot 1 = 2 \). Затем мы определяем \( b: 1 = 2 \cdot 2 + b \), откуда следует \( b = -3 \).
Итак, через точку \( P \) проходит гипербола \( y = \frac{2}{x} \) и прямая \( y = 2x - 3 \).
б
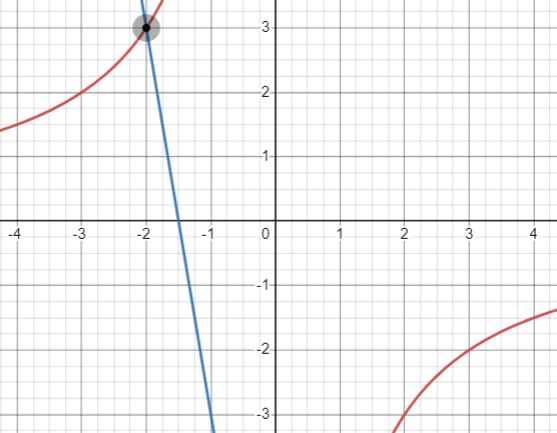
Для точки \( Q \) с координатами \( (-2, 3) \), мы находим произведение \( k = x \cdot y = -2 \cdot 3 = -6 \). Затем мы определяем \( b: 3 = -6 \cdot (-2) + b \), откуда следует \( b = -9 \).
Итак, через точку \( Q \) проходит гипербола \( y = -\frac{6}{x} \) и прямая \( y = -6x - 9 \).
в
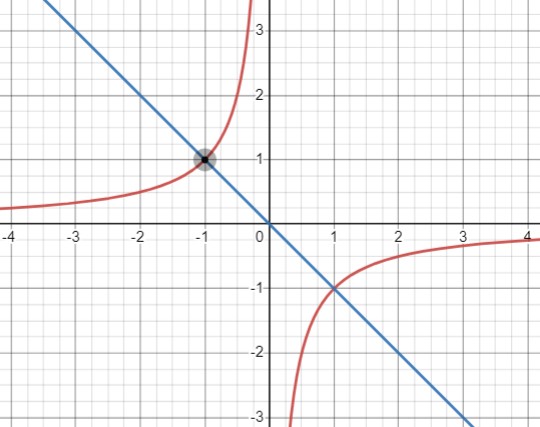
Для точки \( R \) с координатами \( (-1, 1) \), мы находим произведение \( k = x \cdot y = -1 \cdot 1 = -1 \). Затем мы определяем \( b: 1 = -1 \cdot (-1) + b \), откуда следует \( b = 0 \).
Итак, через точку \( R \) проходит гипербола \( y = -\frac{1}{x} \) и прямая \( y = -x \).
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
При каких значениях \(k\) и \(b\) гипербола \(y=\frac{k}{x}\) и прямая \(y=k x+b\) проходят через точку: a) \(P(2 ; 1)\); б) \(Q(-2 ; 3)\); в) \(R(-1 ; 1)\)?
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
