Дополнительные упражнения к главе I — К параграфу 3 — 266 — стр. 63

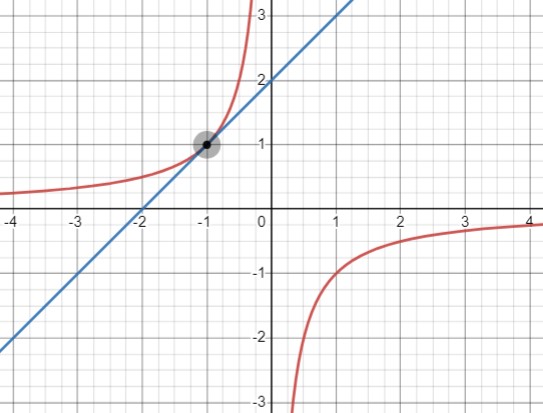
Первым шагом, мы рассматриваем возможность пересечения гиперболы и прямой в одной точке. Это возможно только в том случае, если прямая является касательной к гиперболе. Это происходит, когда уравнение \(\frac{k}{x} = ax + b\) имеет единственный корень, что в свою очередь означает, что дискриминант \(D = b^2 + ak = 0\). Таким образом, мы получаем условие для единственной точки пересечения: \(b^2 = -ak\).

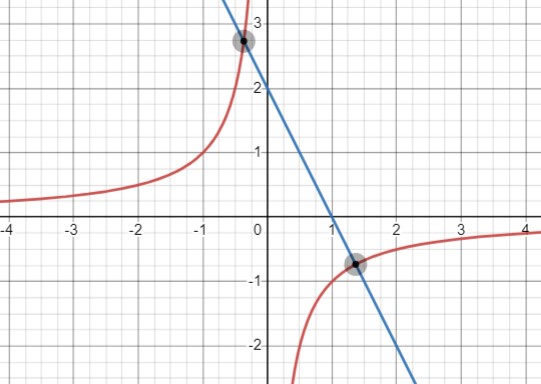
В данном случае рассматривается возможность пересечения гиперболы и прямой в двух точках. Это происходит, когда уравнение \(\frac{k}{x} = ax + b\) имеет два различных корня \(ax^2+bx-k=0\), что соответствует положительному дискриминанту \(D = b^2 + ak > 0\). Это возможно, когда \(k\) и \(a\) имеют одинаковые знаки, обеспечивая два решения для уравнения.

В данном контексте рассматривается невозможность пересечения гиперболы и прямой в трех точках. Это объясняется тем, что квадратное уравнение не может иметь более двух различных корней, что делает невозможным существование трех точек пересечения для гиперболы и прямой.