Дополнительные упражнения к главе V — К параграфу 13 — 1148 — стр. 257

Сначала определим скорость по течению и против течения:
Скорость по течению: \(16 + 4 = 20\) км/ч.
Скорость против течения: \(16 - 4 = 12\) км/ч.

Найдем время на прохождение отрезка \(AB\):
\(\text{Время} = \frac{60}{20} = 3 \text{ часа}\)

Затем найдем время на прохождение отрезка \(BA\):
\(\text{Время} = \frac{60}{15} = 5 \text{ часов}\)

Зададим функцию расстояния от точки \(A\) в момент времени \(t\), обозначив её символом \(l(t)\):
\(l(t) = \begin{cases}20t, & t \in [0; 3) \\60, & t \in [3; 5) \\120 - 12t, & t \in [5; 10]\end{cases}\)

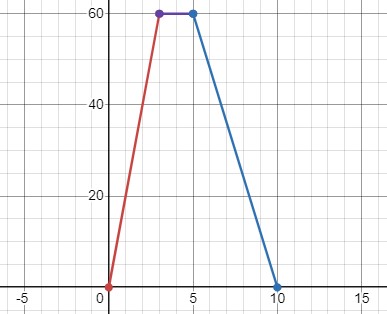
Анализируя функцию \(l(t)\):
При \(t \in [0; 3)\) функция возрастает, так как катер движется по течению реки и отдаляется от точки \(A\), достигая в конце пути точки \(B\).
При \(t \in [3; 5)\) катер стоит на стоянке в пункте \(B\).
При \(t \in [5; 10)\) расстояние от катера до точки \(A\) уменьшается, так как он возвращается обратно к \(A\).

Таким образом, функция \(l(t)\) описывает изменение расстояния между точкой \(A\) и катером в зависимости от времени \(t\).