В одной системе координат постройте графики функций
\(y=\frac{1}{x}, y=\frac{4}{x}, y=-\frac{2}{x}, y=-\frac{6}{x}\)
Как зависит расположение графика функции \(y=\frac{k}{x}\) от модуля коэффициента \(k\)?
В данном утверждении подчеркивается связь между значением параметра \( k \) и расположением ветвей гиперболы. Чем больше модуль значения \( k \), тем более вытянутой и удаленной друг от друга будут ветви гиперболы. Это свойство позволяет оценить форму гиперболы по значению параметра \( k \).
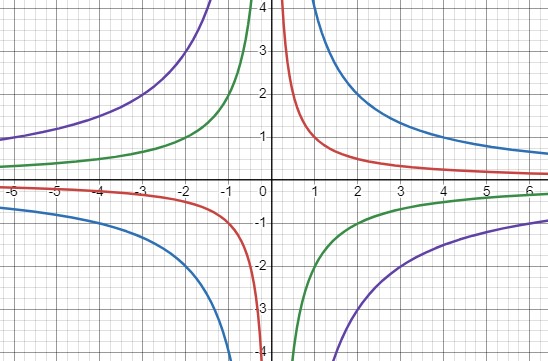
\(y=\frac{1}{x}\) красный
\(y=\frac{4}{x}\) синий
\(y=-\frac{2}{x}\) зеленый
\( y=-\frac{6}{x}\) фиолетовый.
Решебник
"Алгебра - Учебник" по предмету Алгебра за 8 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
В одной системе координат постройте графики функций \(y=\frac{1}{x}, y=\frac{4}{x}, y=-\frac{2}{x}, y=-\frac{6}{x}\) Как зависит расположение графика функции \(y=\frac{k}{x}\) от модуля коэффициента \(k\)?
Еще решебники за 8 класс
Мы подобрали сборники ГДЗ за 8 класс, которые могут быть Вам интересны.
