§10. Геометрическая прогрессия — 30. Формула суммы первых n членов геометрической прогрессии — 628 — стр. 178

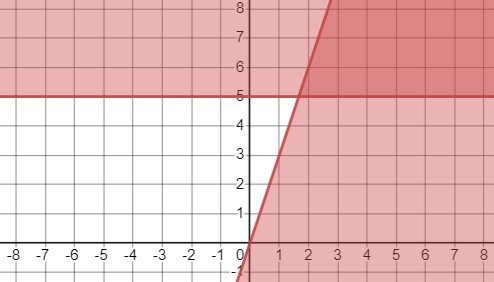
Рассмотрим систему неравенств:
\(\begin{cases}3x - y \geq 0, \\y - 5 \geq 0\end{cases}\)
Приведем ее к более простому виду:
\(\begin{cases}y \leq 3x, \\y \geq 5\end{cases}\)
Таким образом, у нас есть два неравенства: \(y \leq 3x\) и \(y \geq 5\). Это представляет два графика на координатной плоскости.
График уравнения \(y = 3x\) - это линия, а горизонтальная линия \(y = 5\).
Теперь, рассматривая оба графика, можем определить область, которая соответствует выполнению обоих неравенств.
Ответ: Область, удовлетворяющая системе неравенств, - это пространство между линиями.