Постройте график функции и опишите её свойства:
a) \(y=-3x+1\)
б) \(y=5+2x\);
в) \(y=-\frac{3}{x}\);
г) \(y=\frac{1}{2x}\);
д) \(y=-x^{2}\);
е) \(y=-x^{3}\).
\(y=-3x+1\)
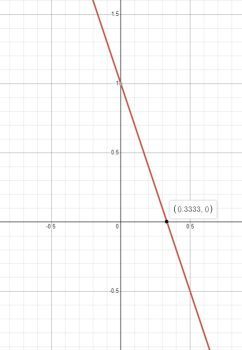
Прямая
x | 0 | 1/3
y | 1 | 0
Область определения:
\(D(f)=(-\infty ;+\infty)\)
Множество значений:
\(E(f)=(-\infty ;+\infty)\)
Нули функции: \(x=\frac{1}{3}\)
Промежутки знакопостоянства:
\(f(x)>0 \text { при } x \in\left(-\infty ; \frac{1}{3}\right) \\ f(x)<0 \text { при } x \in\left(\frac{1}{3} ;+\infty\right)\)
Промежутки монотонности: убывает на всей области определения
Экстремумы: \(y_{\min }-\) нет, \(y_{\max }-\) нет
Чётность/нечётность:
ни чётная, ни нечётная.
\(y=5+2x\)
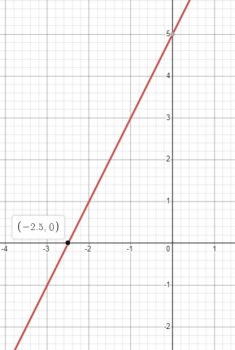
Прямая
x | 0 | -2,5
y | 5 | 0
Область определения:
\(D(f)=(-\infty ;+\infty)\)
Множество значений:
\(E(f)=(-\infty ;+\infty)\)
Нули функции: \(x=-2,5\)
Промежутки знакопостоянства:
\(f(x)>0 \text { при } x \in(-2,5 ;+\infty) \\ f(x)<0 \text { при } x \in(-\infty ; 2,5)\)
Промежутки монотонности: возрастает на всей области определения
Экстремумы: \(y_{\min }-\) нет, \(y_{\max }-\) нет
Чётность/нечётность:
ни чётная, ни нечётная.
\(y=-\frac{3}{x}\)
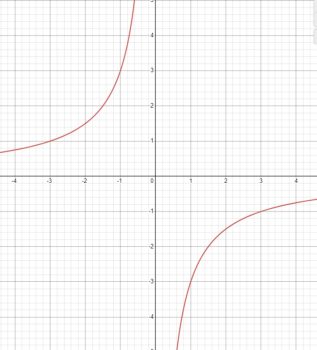
Гипербола, \(k=-3<0\), во 2 и 4 четверти.
Правая ветка
x | 0 | 1,5 | 2 | 3
y | -3 | -2 | -1.5 | -1
Область определения: \(D(f)=(-\infty ; 0) \cup(0 ;+\infty)\)
Множество значений: \(E(f)=(-\infty ; 0) \cup(0 ;+\infty)\)
Нули функции: нет
Промежутки знакопостоянства:
\(f(x)>0 \text { при } x<0, f(x)<0 \text { при } x>0\)
Промежутки монотонности: возрастает на всей области определения
Экстремумы: \(y_{\min }-\) нет, \(y_{\max }-\) нет
Чётность/нечётность: \(f(-x)=-f(x)\) - нечётная.
\(y=\frac{1}{2 x}\)
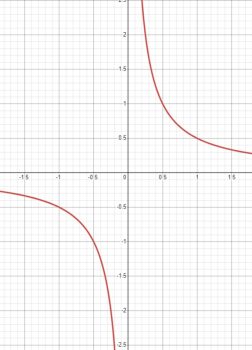
Гипербола, \(k=\frac{1}{2}>0\), в 1 и 3 четверти.
Правая ветка
x | \( \frac{1}{4} \) |\( \frac{1}{2} \) | 1 | 2
y | 2 | 1 | \( \frac{1}{2} \) | \( \frac{1}{4} \)
Область определения: \(D(f)=(-\infty ; 0) \cup (0 ;+\infty)\)
Множество значений: \(E(f)=(-\infty ; 0) \cup (0 ;+\infty)\)
Нули функции: нет
Промежутки знакопостоянства:
\(f(x)>0 \text { при } x>0, \quad f(x)<0 \text { при } x<0\)
Промежутки монотонности: убывает на всей области определения
Экстремумы: \(y_{\min }-\) нет, \(y_{\max }-\) нет
Чётность/нечётность: \(f(-x)=-f(x)\) - нечётная.
\(y=-x^2\)
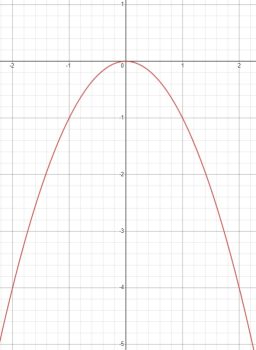
Парабола, \(a=-1<0\) - ветки вниз
Вершина \((0 ; 0)\), ось \(x=0\)
Правая ветка
x |0 |1 | 2 | 3
y | 0 | -1 |-4 | -9
Область определения: \(D(f)=(-\infty;+\infty)\)
Множество значений: \(E(f)=(-\infty; 0]\)
Нули функции: \(x=0\)
Промежутки знакопостоянства: \(f(x)<0\) при \(x \neq 0\)
Экстремумы: \(y_{\min }-\) нет, \(y_{\max }-\) 0
Чётность/нечётность: \(f(-x)=f(x)\) - чётная.
\(y=-x^3\)
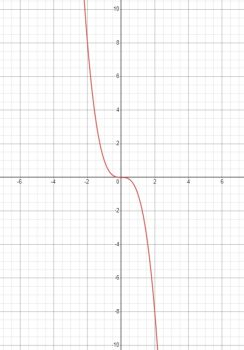
Кубическая парабола, \(a=-1<0\) - в 2 и 4 четвертях
Правая ветка
x |0 |1 | 2 | 3
y | 0 | -1 |-8 | -27
Область определения: \(D(f)=(-\infty;+\infty)\)
Множество значений: \(E(f)=(-\infty;+\infty)\)
Нули функции: \(x=0\)
Промежутки знакопостоянства: \(f(x)>0\) при \(x < 0, f(x)<0\) при \(x > 0\)
Экстремумы: \(y_{\min }-\) нет, \(y_{\max }-\) нет
Чётность/нечётность: \(f(-x)=-f(x)\) - нечётная.
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Постройте график функции и опишите её свойства: a) \(y=-3x+1\) б) \(y=5+2x\); в) \(y=-\frac{3}{x}\); г) \(y=\frac{1}{2x}\); д) \(y=-x^{2}\); е) \(y=-x^{3}\).

