Алгебра
2023
Изобразите схематически график каждой функции (отметьте вершину параболы и направление её ветвей):
a) \(y=\frac{1}{2} x^{2}; y=\frac{1}{2} x^{2}+4; y=\frac{1}{2} x^{2}-3\);
б) \(y=-\frac{1}{3} x^{2}; y=-\frac{1}{3} x^{2}+2; y=-\frac{1}{3} x^{2}-1\);
в) \(y=\frac{1}{5} x^{2}; y=\frac{1}{5}(x-3)^{2}; y=\frac{1}{5}(x+3)^{2}\).
а
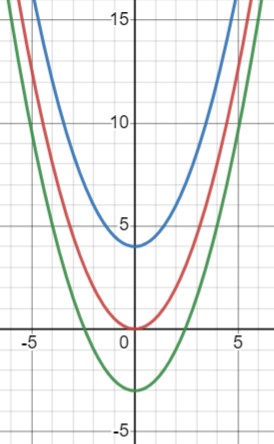
\(y=\frac{1}{2}x^{2}\) - вершина в точке (0,0), ветви вверх.
\(\frac{x}{y}|\frac{-2}{2}|\frac{0}{0}|\frac{1}{0.5}|\frac{3}{4.5}\)
\(y=\frac{1}{2}x^{2}+4\) - вершина в точке (0,4), ветви вверх.
\(y=\frac{1}{2}x^{2}-3\) - вершина в точке (0,-3), ветви вверх.
б
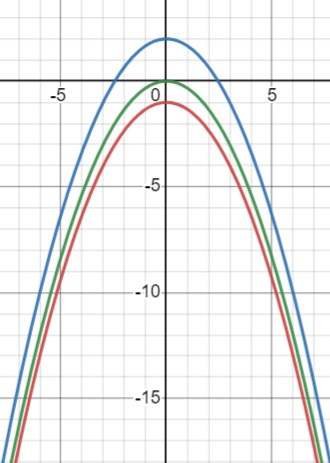
\(y=-\frac{1}{3}x^{2}\) - вершина в точке (0,0), ветви вниз.
\(\frac{x}{y}|\frac{-3}{-3}|\frac{0}{0}|\frac{1}{\frac{1}{3}}|\frac{3}{-3}\)
\(y=-\frac{1}{3}x^{2}+2\) - вершина в точке (0,2), ветви вниз.
\(y=-\frac{1}{3}x^{2}-1\) - вершина в точке (0,-1), ветви вниз.
в
\(y=\frac{1}{5}x^{2}\) - вершина в точке (0,0), ветви вверх.
\(\frac{x}{y}|\frac{-2}{5}|\frac{0}{0}|\frac{1}{1.2}|\frac{3}{0.8}\)
\(y=\frac{1}{5}(x-3)^{2}\) - вершина в точке (3,0), ветви вверх.
\(y=\frac{1}{5}(x+3)^{2}\) - вершина в точке (-3,0), ветви вверх.
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Изобразите схематически график каждой функции (отметьте вершину параболы и направление её ветвей): a) \(y=\frac{1}{2} x^{2}; y=\frac{1}{2} x^{2}+4; y=\frac{1}{2} x^{2}-3\); б) \(y=-\frac{1}{3} x^{2}; y=-\frac{1}{3} x^{2}+2; y=-\frac{1}{3} x^{2}-1\); в) \(y=\frac{1}{5} x^{2}; y=\frac{1}{5}(x-3)^{2}; y=\frac{1}{5}(x+3)^{2}\).
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
