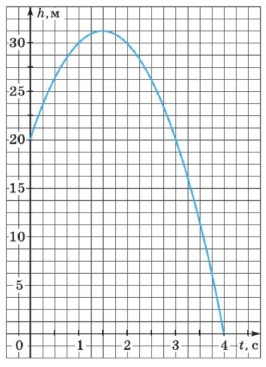
На рисунке 29 изображён график функции \(f(x)=ax^{2}-b\). Найдите, при каком значении \(x\) значение функции равно 68.
\(f(x) = ax^2 - b\)
Вершина параболы \((0, -4)\) \(\Rightarrow b = 4\)
\(f(x) = ax^2 - 4 \)
Точка, принадлежащая графику \((5, 5)\):
\( 5 = a \cdot 5^2 - 4 \Rightarrow a = \frac{5 + 4}{25} = \frac{9}{25} \)
\( f(x) = \frac{9}{25} x^2 - 4 \)
\( \frac{9}{25} x^2 - 4 = 68 \Rightarrow \frac{9}{25} x^2 = 72 \Rightarrow x^2 = 72 \cdot \frac{25}{9} = 200 \Rightarrow x_{1,2} = \pm 10\sqrt{2} \).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
На рисунке 29 изображён график функции \(f(x)=ax^{2}-b\). Найдите, при каком значении \(x\) значение функции равно 68.

