Квадратичная функция задана формулой:
а) \(y=x^{2}-4x+7\);
б) \(y=-2x^{2}-5x-2\).
Найдите координаты вершины параболы. Наметив на координатной плоскости вершину параболы и её ось симметрии, изобразите схематически график.
а
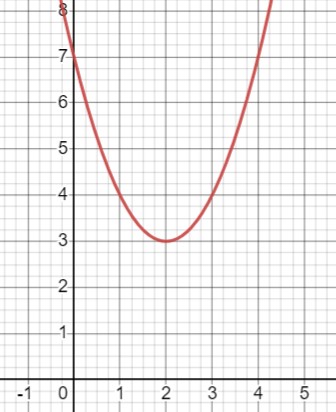
\(y = x^2 - 4x + 7\)
Координаты вершины:
\(x_0 = -\frac{b}{2a} = \frac{4}{2} = 2\\y_0 = 2^2 - 4 \cdot 2 + 7 = 3\)
Ось симметрии \(x = 2\);
\(\frac{x}{y}|\frac{2}{3}|\frac{3}{4}|\frac{4}{7}\)
б
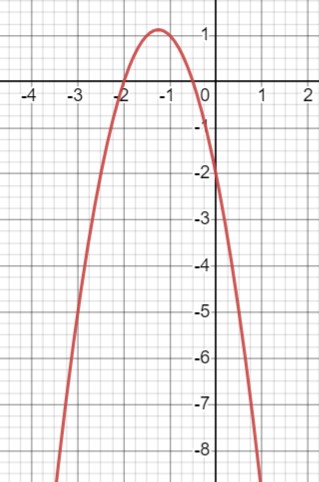
\(y = -2x^2 - 5x - 2\)
Координаты вершины:
\(x_0 = -\frac{b}{2a} = -\frac{5}{4} = -1 \frac{1}{4}\\y_0 = -2 \cdot \left(-\frac{5}{4}\right)^2 - 5 \cdot \left(-\frac{5}{4}\right) - 2 = \frac{9}{8} = 1 \frac{1}{8}\)
Ось симметрии \(x = -1 \frac{1}{4}\);
\(\frac{x}{y}|\frac{-1 \frac{1}{4}}{1 \frac{1}{8}} \,|\frac{0}{-2} \, |\frac{1}{-9}\)
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Квадратичная функция задана формулой: а) \(y=x^{2}-4x+7\); б) \(y=-2x^{2}-5x-2\). Найдите координаты вершины параболы. Наметив на координатной плоскости вершину параболы и её ось симметрии, изобразите схематически график.
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
