Вертикаль
2016
Постройте график функции \(y=2x^{2}+8x+2\) и найдите, используя график:
а) значения у при \(x=-2,3 ;-0,5 ; 1,2\);
б) значения \(x\), при которых \(y=-4 ;-1 ; 1,7\);
в) нули функции и промежутки знакопостоянства;
г) промежутки возрастания и убывания функции, наименьшее значение функции.
\(x_{0}=-\frac{8}{2 \cdot 2}=-2; \)
\(y_{0}=2 \cdot(-2)^{2}+8 \cdot(-2)+2=-6; \)
\(y=2 x^{2}+8 x+2=2(x+2)^{2}-6\)
\(\frac{x}{y}|\frac{-2}{-6}|\frac{0}{2}|\frac{1}{12}\)
а
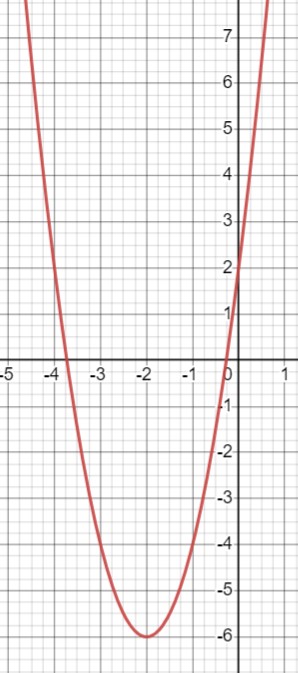
\(y(-2,3) \approx -5,7\)
\(y(-0,5) \approx -1,5\)
\(y(1,2) \approx 14\).
б
\(y=-4\) при \(x-3\) и \(x=-1\)
\(y=-1\) при \(x \approx -3,6\) и \(x \approx -0,4\)
\(y=1,7\) при \(x \approx -4\) и \(x \approx 0\).
в
\(y=0\) при \(x \approx -3,8\) и \(x \approx -0,2\)
\(y>0\) при \(x \in (-\infty ;-3,8) \cup (-0,2 ;+\infty)\)
\(y<0\) при \(x \in (-3,8 ;-0,2)\).
г
Функция убывает при \(x \in (-\infty ;-2]\)
Функция возрастает при \(x \in [-2 ;+\infty)\)
Наименьшее значение функции: \(y=-6\).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Постройте график функции \(y=2x^{2}+8x+2\) и найдите, используя график: а) значения у при \(x=-2,3 ;-0,5 ; 1,2\); б) значения \(x\), при которых \(y=-4 ;-1 ; 1,7\); в) нули функции и промежутки знакопостоянства; г) промежутки возрастания и убывания функции, наименьшее значение функции.
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
