§4. Квадратичная функция и ее график — 11. Построение графика квадратичной функции — 153 — стр. 60

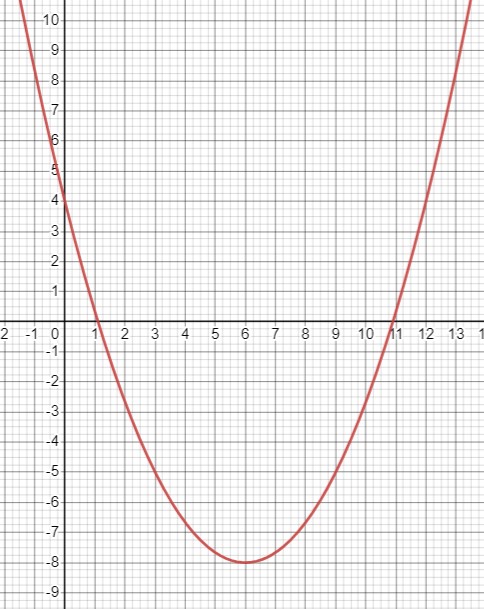
\(y=\frac{1}{3} x^{2}-4 x+4\)

Вершина находится в этих координатах:

\(x_{0}=-\frac{-4}{\frac{2}{3}}=6\),

\(y_{0}=\frac{1}{3} \cdot 6^{2}-4 \cdot 6+4=-8\);

\(y=\frac{1}{3}(x-6)^{2}-8\);

Область определения: \(x \in R\);

Область значений: \(y \in[-8 ;+\infty)\);

Промежутки возрастания: \(x \in[6 ;+\infty)\);

Промежутки убывания: \(x \in(-\infty ; 6]\);

\(y>0\) при \(x \in(-\infty ; 1,1) \cup(10,9 ;+\infty)\)

\(y<0\) при \(x \in(1,1 ; 10,9)\);

Наименышее значение: \(y=-8\).

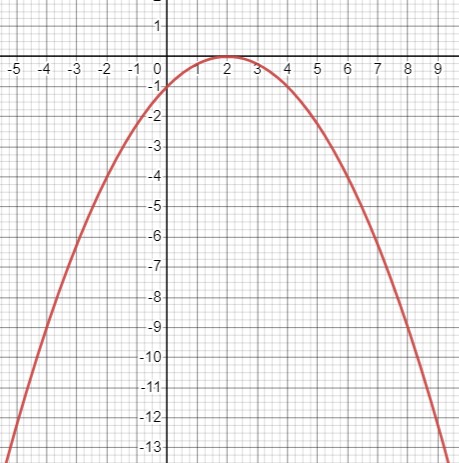
\(y=-\frac{1}{4} x^{2}+x-1\)

Вершина находится в этих координатах:

\(x_{0}=-\frac{1}{\frac{2}{4}}=2\),

\(y_{0}=-\frac{1}{4} \cdot 2^{2}+2-1=0\)

\(y=-\frac{1}{4}(x-2)^{2}\);

Область определения: \(x \in R\),

Область значений: \(y \in(-\infty ; 0]\);

Промежутки возрастания: \(x \in(-\infty ; 2]\);

Промежутки убывания: \(x \in[2 ;+\infty)\);

\(y<0\) при \(x \in(-\infty ; 2) \cup(2 ;+\infty)\),

Наибольшее значение: \(y=0\);

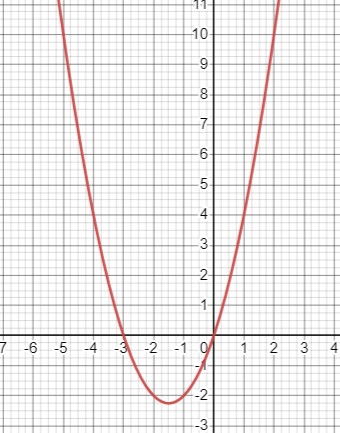
\(y=x^{2}+3 x\)

Вершина находится в этих координатах:

\(x_{0}=-\frac{3}{2}\),

\(y_{0}=\left(-\frac{3}{2}\right)^{2}+3 \cdot\left(-\frac{3}{2}\right)=-\frac{9}{4}=-2 \frac{1}{4}\);

\(y=(x+1,5)^{2}-2,25\);

Область определения: \(x \in R\),

Область значений: \(y \in[-2,25 ;+\infty)\)

Промежутки возрастания: \(x \in[-1,5 ;+\infty)\);

Промежутки убывания: \(x \in(-\infty ;-1,5]\);

\(y>0\) при \(x \in(-\infty ;-3) \cup(0 ;+\infty)\);

\(y<0\) при \(x \in(-3 ; 0)\);

Наименьшее значение: \(y=-2,25\),