§4. Квадратичная функция и ее график — 12. Дробно-линейная функция и её график — 172 — стр. 67

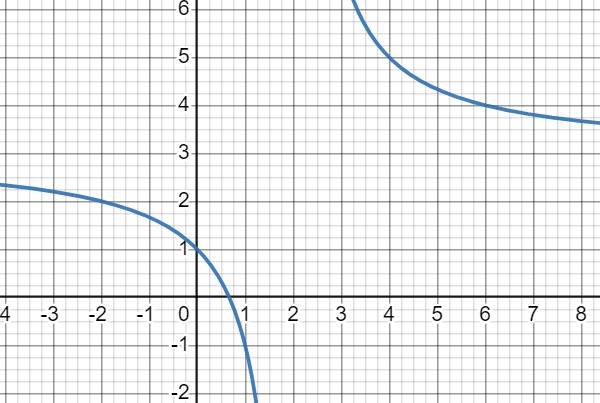
\(y=\frac{3 x-2}{x-2}=\frac{3(x-2)+4}{x-2}=3+\frac{4}{x-2}\)
Область определения: \(x \neq 2\);
Асимптоты: \(x=2\), \(y=3\);
\(\frac{x}{y}|\frac{-2}{2}|\frac{0}{1}|\frac{1}{-1}|\frac{3}{7}|\frac{4}{5}|\frac{6}{4}\)
Нули функции:
\(3 x-2=0\),
\(x=\frac{2}{3}\)
Промежутки знакопостоянства:
\(y>0\) при \(x \in(-\infty, \frac{2}{3}) \cup (2,+\infty)\);
\(y<0\) при \(x \in(\frac{2}{3}, 2)\).