§4. Квадратичная функция и ее график — 12. Дробно-линейная функция и её график — 176 — стр. 67

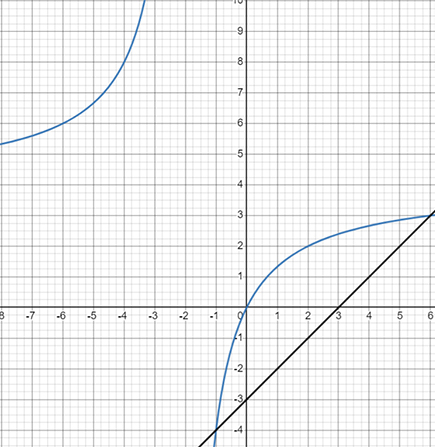
\(y=\frac{4 x}{x+2}=x-3\)
\(y=\frac{4 x}{x+2}\);
\(y=\frac{4(x+2)-8}{x+2}=4-\frac{8}{x+2}\)
Асимптоты: \(x=-2\), \(y=4\);
\(\frac{x}{y}|\frac{-6}{6}|\frac{-4}{8}|\frac{-3}{12}|\frac{-1}{-4}|\frac{0}{0}|\frac{2}{2}\)
\(y=x-3-\) прямая;
\(\frac{x}{y}|\frac{-1}{4}|\frac{0}{-3}|\frac{3}{0}\)
Есть 2 точки пересечения: \(x_{1}=-1, x_{2}=6\).