Постройте график функции \(g(x)=\frac{6}{|x-2|}\). Решите уравнение:
а) \(g(x)=3\);
б) \(g(x)=6\);
в) \(g(x)=-2\).
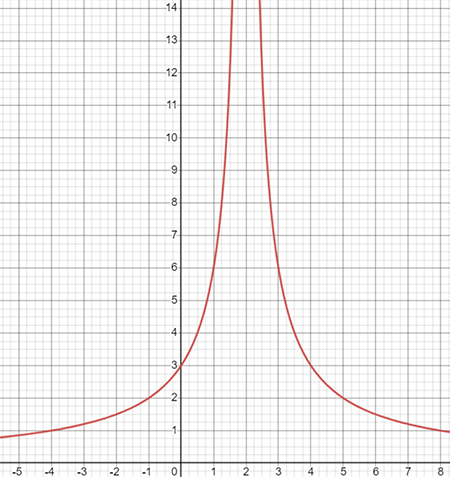
\(\frac{x}{y}|\frac{-4}{1}|\frac{0}{3}|\frac{1}{6}|\frac{3}{6}|\frac{4}{3}|\frac{5}{2}\).
\(g(x) = 3\)
Ищем точки пересечения графика и горизонтальной линии \(y = 3\):
\( \frac{6}{|x - 2|} = 3 \)
Решая это уравнение, получим две возможные точки:
\( |x - 2| = 2 \)
1. \(x - 2 = 2\), тогда \(x = 4\)
2. \(2 - x = 2\), тогда \(x = 0\).
\(g(x) = 6\)
\( \frac{6}{|x - 2|} = 6 \)
Решая это уравнение, получим одну точку:
\( |x - 2| = 1 \)
1. \(x - 2 = 1\), тогда \(x = 3\).
\(g(x) = -2\)
\(\frac{6}{|x - 2|} = -2 \)
Это уравнение не имеет решений, так как выражение \(\frac{6}{|x - 2|}\) всегда положительно, а \(-2\) отрицательно. Таким образом, уравнение \(g(x) = -2\) не имеет решений.
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Постройте график функции \(g(x)=\frac{6}{|x-2|}\). Решите уравнение: а) \(g(x)=3\); б) \(g(x)=6\); в) \(g(x)=-2\).

