§4. Квадратичная функция и ее график — 9. Функция, её график и свойства — 120 — стр. 48

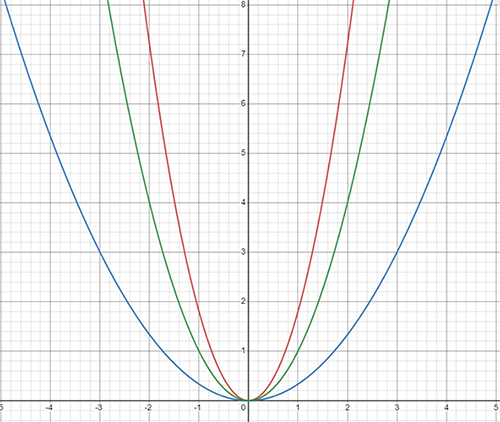
\(y=x^2\) - зеленый график;
\(\frac{x}{y}|\frac{-1}{1}|\frac{0}{0}|\frac{1}{1}|\frac{2}{4}\)
\(y=1,8 x^2\) - красный график;
\(\frac{x}{y}|\frac{-1}{1.8}|\frac{0}{0}|\frac{1}{1.8}|\frac{2}{7.2}\)
\(y=\frac{1}{3} x^2\) - синий график;
\(\frac{x}{y}|\frac{-1}{\frac{1}{3}}|\frac{0}{0}|\frac{1}{\frac{1}{3}}|\frac{2}{\frac{4}{3}}\)

Значения функции \(y=1,8 x^2\) в заданных точках больше значений функции \(y=x^2\) в тех же точках, а они, в свою очередь, больше значений функции \(y=\frac{1}{3} x^2\) в тех же точках.