§4. Квадратичная функция и ее график — 9. Функция, её график и свойства — 126 — стр. 49

\(-x^2=2 x-3 \\ x^2+2 x-3=0 \\ x_{1,2}=\frac{-2 \pm \sqrt{4+12}}{2} \\ x_1=1 \\ x_2=-3 \\ y(1)=-1 \\ y(-3)=-9\)
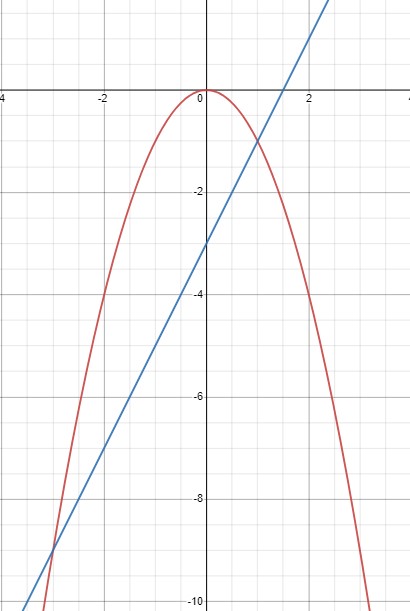
\(y=-x^2\)- красный график;
\(\frac{x}{y}|\frac{-3}{-9}|\frac{0}{0}|\frac{1}{-1}|\frac{2}{-4}\)

\(y=2 x-3\)- синий график.
\(\frac{x}{y}|\frac{-3}{-9}|\frac{0}{-3}|\frac{1}{-1}|\frac{2}{1}\).