§4. Квадратичная функция и ее график — Дополнительные упражнения к параграфу 3 — 182 — стр. 68

Функция $y=\sqrt{kx}$ представляет собой корень из произведения коэффициента $k$ и переменной $x$. Давайте рассмотрим, как меняется характер графика в зависимости от значения коэффициента $k$:

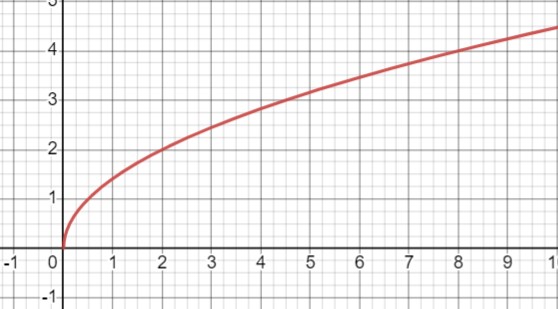
а) Когда $k=2$:
$y=\sqrt{2x}$
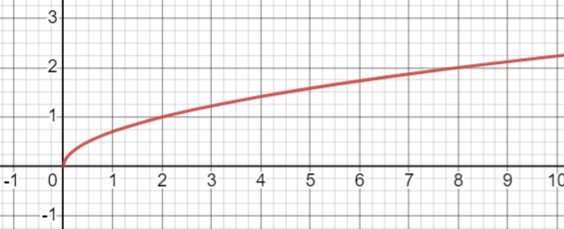
б) Когда $k=0.5$:
$y=\sqrt{0.5x}$

Общий характер графика при различных значениях $k$ будет следующим:

1. Параметр $k$ влияет на наклон и форму графика. Большие значения $k$ увеличивают скорость роста графика, делая его более крутым, а малые значения $k$ делают график более пологим.
2. Если $k>1$, график будет более крутым и стремиться к вертикальной оси.
3. Если $0<k<1$, график будет пологим и стремиться к горизонтальной оси.
4. Если $k=0$, график будет находиться на оси $y$ (горизонтальной оси).
5. Если $k<0$, функция не определена для отрицательных значений $x$, так как корень из отрицательного числа не существует в действительных числах.

Таким образом, параметр $k$ в функции $y=\sqrt{kx}$ влияет на наклон и общую форму графика, определяя, насколько быстро он растет или убывает в зависимости от значений $x$.