§4. Квадратичная функция и ее график — Дополнительные упражнения к параграфу 3 — 184 — стр. 68

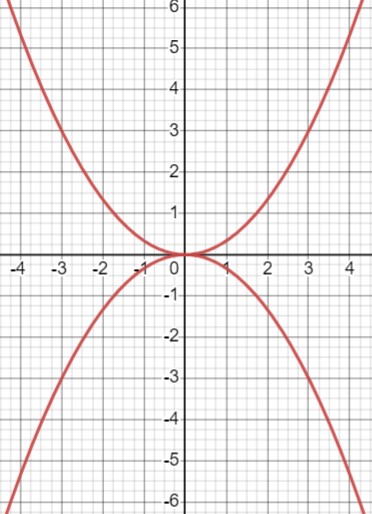
Функция \(y = ax^2\), где \(a > 0\):

Область определения: \(D(f) = (-\infty; +\infty)\)

Множество значений: \(E(f) = [0; +\infty)\)

Нули функции: \(x = 0\)

Промежутки знакопостоянства: \(f(x) > 0 \text { при } x \neq 0\)

Промежутки монотонности: убывает при \(x \leq 0\), возрастает при \(x \geq 0\)

Экстремумы: \(y_{\min} = 0\), \(y_{\max} -\) нет

Чётность/нечётность: \(f(-x) = f(x) \text { - чётная}\).

Функция \(y = ax^2\), где \(a < 0\):

Область определения: \(D(f) = (-\infty; +\infty)\)

Множество значений: \(E(f) = (-\infty; 0]\)

Нули функции: \(x = 0\)

Промежутки знакопостоянства: \(f(x) < 0 \text { при } x \neq 0\)

Промежутки монотонности: возрастает при \(x \leq 0\), убывает при \(x \geq 0\)

Экстремумы: \(y_{\min} -\) нет, \(y_{\max} = 0\)

Чётность/нечётность: \(f(-x) = f(x) \text { - чётная}\).