Постройте график функции, заданной формулой \(y=-0.25x^{2}\), где \(x \in[-6; 2]\). Каковы наибольшее и наименьшее значения этой функции?
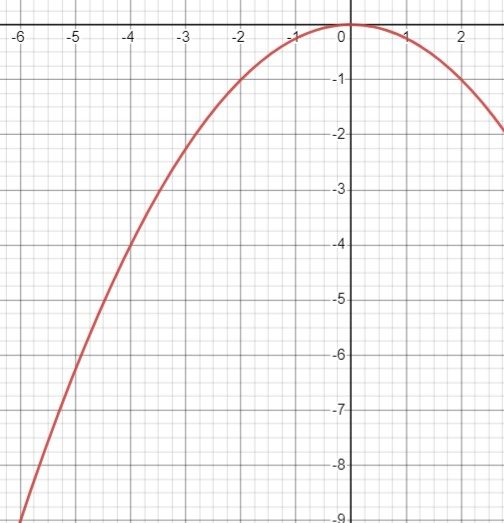
\(y = -0.25x^2 \)
Парабола, ветви вниз.
Область определения: \( x \in [-6, 2] \).
Координаты вершины параболы:
\(x = -\frac{b}{2a} = 0 \\y(0) = 0\)
Значения функции в крайних точках области определения:
\(y(-6) = -0.25 \cdot 36 = -9 \\y(2) = -0.25 \cdot 4 = -1\)
\(\frac{x}{y}|\frac{-6}{-9}|\frac{-2}{-1}|\frac{0}{0}|\frac{2}{-1}\)
Наибольшее значение функции: \(y = 0\);
Наименьшее значение функции: \(y = -9\).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Постройте график функции, заданной формулой \(y=-0.25x^{2}\), где \(x \in[-6; 2]\). Каковы наибольшее и наименьшее значения этой функции?
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
