§5. Уравнения с одной переменной — 15. Решение задач с помощью уравнений — 263 — стр. 87

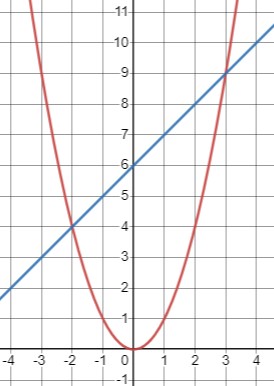
Для решения уравнения \(x^2 - x - 6 = 0\) можно воспользоваться графиками функций \(y=x^2\) и \(y=x+6\).
1. График функции \(y=x^2\):
Это парабола, открывающаяся вверх. Уравнение \(y=x^2\) имеет корни при \(x=3\) и \(x=-3\), так как \(3^2 = 9\) и \((-3)^2 = 9\).
2. График функции \(y=x+6\):
Это прямая линия с наклоном 1 и точкой пересечения с осью y при \(y=6\).
Теперь рассмотрим, где графики пересекаются. Пересечение графиков происходит в точках, где значения y для обеих функций одинаковы. Таким образом, решения уравнения \(x^2 - x - 6 = 0\) можно найти в точках пересечения графиков \(y=x^2\) и \(y=x+6\).
Графически можно заметить, что пересечения происходят при \(x = -2\) и \(x = 3\). Подставим эти значения в уравнение:
1. При \(x = -2\):
\((-2)^2 - (-2) - 6 = 4 + 2 - 6 = 0\)
2. При \(x = 3\):
\((3)^2 - (3) - 6 = 9 - 3 - 6 = 0\)
Таким образом, уравнение имеет два корня: \(x = -2\) и \(x = 3\).