Физика
2024
Решите неравенство:
а) \(x^{2}+2x-480\);
в) \(-x^{2}+2x+15>0\);
г) \(-5x^{2}+11x-6>0\);
д) \(4x^{2}-12x+9>0\);
е) \(25x^{2}+30x+90\);
з) \(-2x^{2}+7x<0\).
а
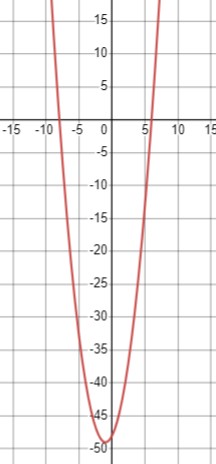
\(x^2+2x-48 < 0\)
Парабола у нас направлена вверх, и для нахождения корней решим уравнение \(x^2+2x-48 = 0\):
\(x_{1,2} = \frac{-2 \pm \sqrt{4+192}}{2}\)
Таким образом, получаем корни:
\(x_1 = 6\)
\(x_2 = -8\)
Следовательно, решение неравенства \(x \in (-8; 6)\).
б
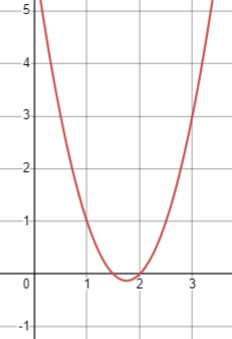
\(2x^2-7x+6 > 0\)
Парабола направлена вверх, и решение будем искать из уравнения \(2x^2-7x+6 = 0\):
\(x_{1,2} = \frac{7 \pm \sqrt{49-48}}{4}\)
Отсюда получаем корни:
\(x_1 = 2\)
\(x_2 = \frac{3}{2}\)
Таким образом, решение неравенства \(x \in \left(-\infty; \frac{3}{2}\right) \cup (2; +\infty)\).
в
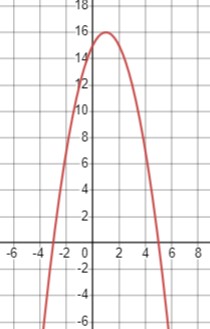
\(-x^2+2x+15 < 0\)
Парабола направлена вниз, и для нахождения корней решим уравнение \(-x^2+2x+15 = 0\):
\(x_{1,2} = \frac{-2 \pm \sqrt{4+60}}{-2}\)
Получаем корни:
\(x_1 = -3\)
\(x_2 = 5\)
Следовательно, решение неравенства \(x \in (-\infty; -3) \cup (5; +\infty)\).
г
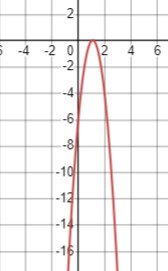
\(-5x^2+11x-6 > 0\)
Парабола направлена вниз, и решение будем искать из уравнения \(-5x^2+11x-6 = 0\):
\(x_{1,2} = \frac{-11 \pm \sqrt{121-120}}{-10}\)
Получаем корни:
\(x_1 = 1\)
\(x_2 = 1,2\)
Следовательно, решение неравенства \(x \in (1; 1,2)\).
д
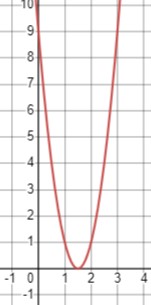
\(4x^2-12x+9 > 0\)
Парабола направлена вверх, и решение будем искать из уравнения \(4x^2-12x+9 = 0\):
\(x_{1,2} = \frac{12 \pm \sqrt{144-144}}{8}\)
Получаем корень:
\(x = \frac{3}{2}\)
Таким образом, решение неравенства \(x \in \left(-\infty; 1 \frac{1}{2}\right) \cup \left(1 \frac{1}{2}; +\infty\right)\).
е
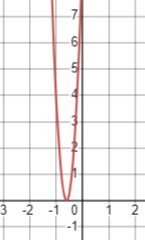
\(25x^2+30x+9 < 0\)
Парабола направлена вверх, и решение будем искать из уравнения \(25x^2+30x+9 = 0\). Дискриминант этого уравнения равен нулю, что говорит о том, что парабола не пересекает ось \(Ox\), и у уравнения нет корней. Следовательно, решений нет.
ж
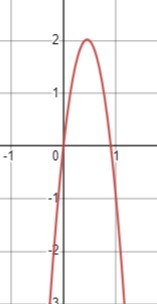
\(-10x^2+9x > 0\)
Парабола направлена вниз, и решение будем искать из уравнения \(-10x^2+9x = 0\):
\(x(9-10x) = 0\)
Получаем корни:
\(x_1 = 0\)
\(x_2 = \frac{9}{10}\)
Следовательно, решение неравенства \(x \in \left(0; \frac{9}{10}\right)\).
з
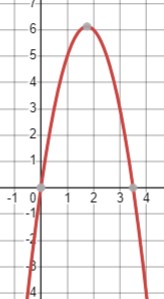
\(-2x^2+7x < 0\)
Парабола направлена вниз, и решение будем искать из уравнения \(-2x^2+7x = 0\):
\(x(7-2x) = 0\)
Получаем корни:
\(x_1 = 0\)
\(x_2 = \frac{7}{2}\)
Следовательно, решение неравенства \(x \in (-\infty; 0) \cup \left(\frac{7}{2}; +\infty\right)\).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Решите неравенство: а) \(x^{2}+2x-480\); в) \(-x^{2}+2x+15>0\); г) \(-5x^{2}+11x-6>0\); д) \(4x^{2}-12x+9>0\); е) \(25x^{2}+30x+90\); з) \(-2x^{2}+7x<0\).
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
