Алгебра
2023
Решите неравенство:
а) \(2x^{2}+13x-7>0\);
б) \(-9x^{2}+12x-4<0\);
в) \(6x^{2}-13x+5\leq 0\);
г) \(-2x^{2}-5x+18\leq 0\);
д) \(3x^{2}-2x>0\);
е) \(8-x^{2}<0\).
а
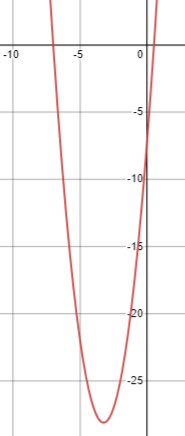
\(2 x^2+13 x-7>0\)
Решим уравнение \(2 x^2+13 x-7=0\):
\(x_{1,2} = \frac{-13 \pm \sqrt{13^2-4 \cdot 2 \cdot (-7)}}{4}\)
\(D = 169 + 56 = 225\)
\(x_{1,2} = \frac{-13 \pm \sqrt{225}}{4}\)
\(x_1 = -7\)
\(x_2 = \frac{1}{2}\)
Теперь рассмотрим интервалы между найденными корнями и за пределами:
\(x \in \left(-\infty ; -7\right) \cup \left(\frac{1}{2}; +\infty\right)\)
Итак, множество решений: \(x \in \left(-\infty ; -7\right) \cup \left(\frac{1}{2}; +\infty\right)\).
б
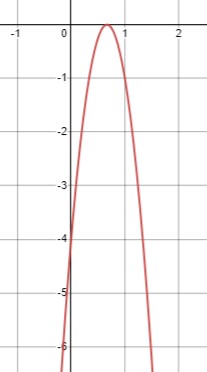
\(-9 x^2+12 x-4<0\)
Решим уравнение \(-9 x^2+12 x-4=0\):
\(x_{1,2} = \frac{-12 \pm \sqrt{12^2-4 \cdot (-9) \cdot (-4)}}{-18}\)
\(D = 144 - 144 = 0\)
\(x = \frac{2}{3}\)
Теперь рассмотрим интервалы между найденными корнями и за пределами:
\(x \in \left(-\infty ; \frac{2}{3}\right) \cup \left(\frac{2}{3}; +\infty\right)\).
в
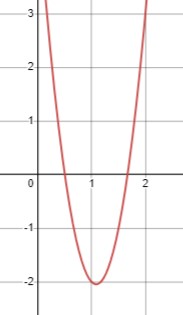
\(6 x^2-13 x+5 \leq 0\)
Решим уравнение \(6 x^2-13 x+5=0\):
\(x_{1,2} = \frac{13 \pm \sqrt{13^2-4 \cdot 6 \cdot 5}}{12}\)
\(D = 169 - 120 = 49\)
\(x_1 = \frac{5}{3}\)
\(x_2 = \frac{1}{2}\)
Теперь рассмотрим интервалы между найденными корнями и за пределами:
\(x \in \left(\frac{1}{2}; \frac{5}{3}\right)\).
г
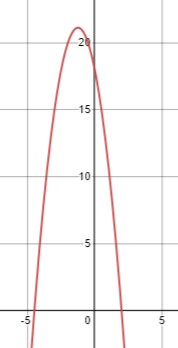
\(-2 x^2-5 x+18 \leq 0\)
Решим уравнение \(-2 x^2-5 x+18=0\):
\(x_{1,2} = \frac{5 \pm \sqrt{5^2+4 \cdot 2 \cdot 18}}{-4}\)
\(D = 25 - 144 = -119\)
Уравнение не имеет вещественных корней.
Таким образом, нам нужно рассмотреть знаки выражения при различных значениях x:
1. \(-\infty < x < -4.5\) - выражение \(-2 x^2-5 x+18\) положительно.
2. \(-4.5 < x 2\) - выражение \(-2 x^2-5 x+18\) положительно.
Таким образом, множество решений: \(x \in (-\infty ;-4.5) \cup (2 ;+\infty)\).
д
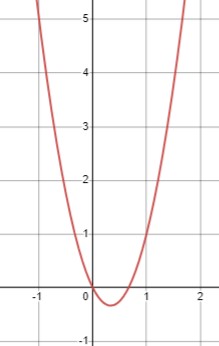
\(3 x^2-2 x>0\)
Решим уравнение \(3 x^2-2 x=0\):
\(x(3 x-2)=0\)
\(x_1 = 0\)
\(x_2 = \frac{2}{3}\)
Теперь рассмотрим интервалы между найденными корнями и за пределами:
\(x \in \left(-\infty ; 0\right) \cup \left(\frac{2}{3} ;+\infty\right)\).
е
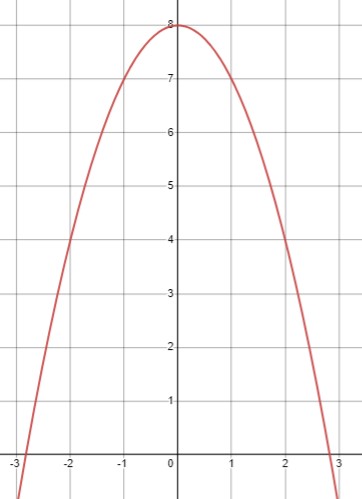
\(8-x^2<0\)
Решим уравнение \(8-x^2=0\):
\(x^2=8\)
\(x = \pm 2 \sqrt{2}\)
Теперь рассмотрим интервалы между найденными корнями и за пределами:
\(x \in \left(-\infty ;-2 \sqrt{2}\right) \cup \left(2 \sqrt{2} ;+\infty\right)\).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Решите неравенство: а) \(2x^{2}+13x-7>0\); б) \(-9x^{2}+12x-4<0\); в) \(6x^{2}-13x+5\leq 0\); г) \(-2x^{2}-5x+18\leq 0\); д) \(3x^{2}-2x>0\); е) \(8-x^{2}<0\).
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
