§6. Неравенства с одной переменной — 16. Решение неравенств второй степени с одной переменной — 267 — стр. 91

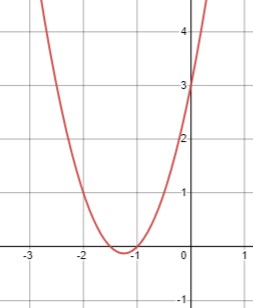
Для неравенства \(2x^2 + 5x + 3 > 0\), найдем корни уравнения \(2x^2 + 5x + 3 = 0\), используя дискриминант: \(x_{1,2}=\frac{-5 \pm \sqrt{25-24}}{4}\), что дает корни \(x_1 = -1\) и \(x_2 = -\frac{3}{2}\). Поскольку ветви параболы направлены вверх, уравнение положительно между корнями. Таким образом, множество решений для данного неравенства \(x \in (-\infty, -1.5) \cup (-1, +\infty)\).

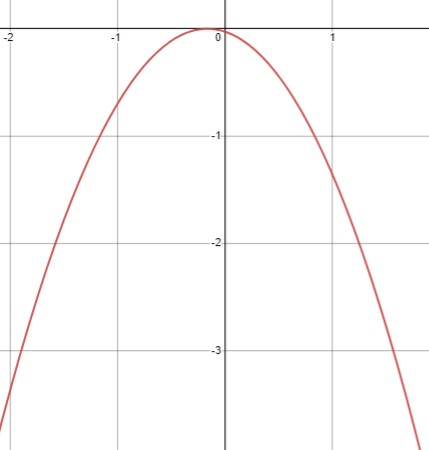
Для неравенства \(-x^2 - \frac{1}{3}x - \frac{1}{36} < 0\), найдем корень уравнения \(-36x^2 - 12x - 1 = 0\), который равен \(x = -\frac{1}{6}\). График параболы касается оси \(x\), и ветви направлены вниз, следовательно, выражение отрицательно между корнем и за его пределами. Таким образом, множество решений для данного неравенства \(x \in (-\infty, -\frac{1}{6}) \cup (-\frac{1}{6}, +\infty)\).