§6. Неравенства с одной переменной — 16. Решение неравенств второй степени с одной переменной — 268 — стр. 91

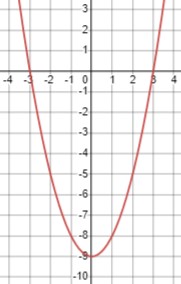
\(x^2 < 16\)

Это неравенство означает, что квадрат \(x\) должен быть меньше 16. Решим его:

\(x^2 < 16\)

\((x-4)(x+4) < 0\)

Таким образом, корни уравнения \(x^2 - 16 = 0\) равны -4 и 4. Поскольку умножение двух чисел с противоположными знаками дает отрицательный результат, то нам нужны значения \(x\) между -4 и 4:

\(x \in (-4, 4)\).

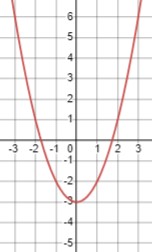
\(x^2 \geq 3\)

Здесь мы ищем значения \(x\), для которых квадрат \(x\) больше или равен 3. Решим:

\(x^2 \geq 3\)

\(x \leq -\sqrt{3} \quad \text{или} \quad x \geq \sqrt{3}\)

Это означает, что \(x\) должен быть меньше или равен \(-\sqrt{3}\) или больше или равен \(\sqrt{3}\):

\(x \in (-\infty, -\sqrt{3}) \cup (\sqrt{3}, +\infty)\).

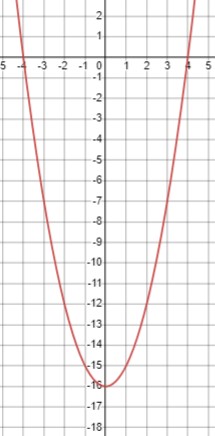
\(0.2x^2 > 1.8\).

Умножим обе части на 5, чтобы избавиться от десятичной дроби:

\(x^2 > 9\)

Теперь найдем корни:

\(x < -3 \quad \text{или} \quad x > 3\)

Таким образом, решение неравенства \(0.2x^2 > 1.8\) это \(x \in (-\infty, -3) \cup (3, +\infty)\).

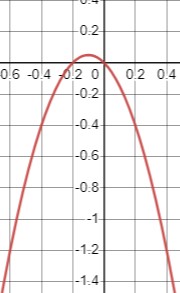
\(-5x^2 \leq x\)

Умножим обе части на -1:

\(5x^2 \geq -x\)

\(5x^2 + x \geq 0\)

\(x(5x + 1) \geq 0\)

Таким образом, уравнение выполняется, когда \(x \leq -\frac{1}{5}\) или \(x \geq 0\):

\(x \in \left(-\infty, -\frac{1}{5}\right) \cup (0, +\infty)\).

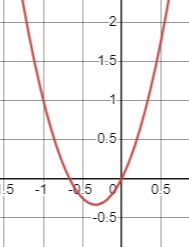
\(3x^2 < -2x\)

Переносим все члены в одну сторону:

\(3x^2 + 2x < 0\)

\(x(3x + 2) < 0\)

Таким образом, уравнение выполняется, когда \(-\frac{2}{3} < x < 0\):

\(x \in \left(-\frac{2}{3}, 0\right)\).

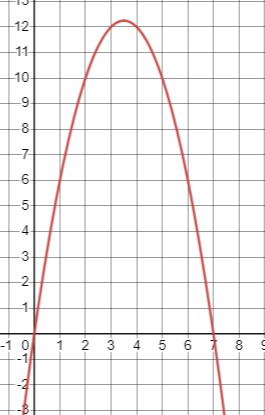
\(7x < x^2\)

Вынесем \(x\) из обеих частей:

\(x(7 - x) < 0\)

Таким образом, уравнение выполняется, когда \(0 < x < 7\):

\(x \in (0, 7)\).