История России
2017
Решите неравенство:
а) \(0,01x^{2}\leq 1\);
б) \(\frac{1}{2}x^{2}>12\);
в) \(4x\leq -x^{2}\)
г) \(\frac{1}{3}x^{2}>\frac{1}{9}\);
д) \(5x^{2}>2x\);
е) \(-0,3x<0,6x^{2}\);
а
\(0.01 x^2 \leq 1\)
Умножим обе части на 100, чтобы избавиться от десятичной дроби:
\(x^2 \leq 100\)
Теперь найдем корни:
\(x \leq -10 \quad \text{или} \quad x \geq 10\)
Таким образом, решение неравенства \(0.01 x^2 \leq 1\) это \(x \in (-10, 10)\).
б
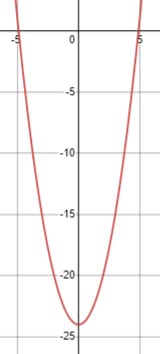
\(\frac{1}{2} x^2 > 12\)
Умножим обе части на 2:
\(x^2 > 24\)
Теперь найдем корни:
\(x > \sqrt{24} \quad \text{или} \quad x > -\sqrt{24}\)
Таким образом, решение неравенства \(\frac{1}{2} x^2 > 12\) это \(x \in (-\infty, -2\sqrt{6}) \cup (2\sqrt{6}, +\infty)\).
в
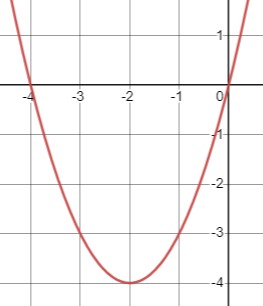
\(4 x \leq -x^2\)
Решим квадратное уравнение:
\(x^2 + 4x \leq 0\)
\(x(x + 4) = 0\)
\(x_1 = 0, \quad x_2 = -4\)
Парабола направлена вверх, и решение уравнения это \(x \in (-4, 0)\).
г
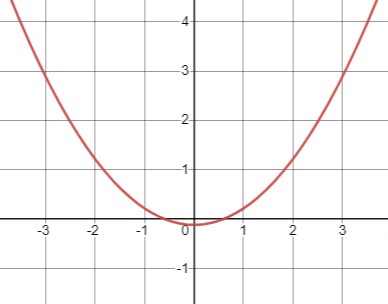
\(\frac{1}{3} x^2 > \frac{1}{9}\)
Умножим обе части на 3:
\(x^2 > \frac{1}{3}\)
Теперь найдем корни:
\(x \in \left(-\infty, -\frac{1}{\sqrt{3}}\right) \cup \left(\frac{1}{\sqrt{3}}, +\infty\right)\).
д
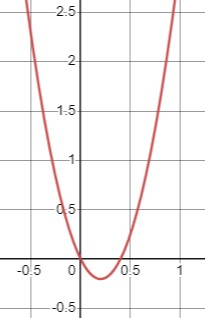
\(5 x^2 > 2 x\)
Решим уравнение:
\(5 x^2 - 2 x > 0\)
\(x(5 x - 2) = 0\)
\(x_1 = 0, \quad x_2 = \frac{2}{5}\)
Парабола направлена вверх, и решение уравнения это \(x \in (-\infty, 0) \cup (\frac{2}{5}, +\infty)\).
е
\(-0.3 x < 0.6 x^2\)
Решим уравнение:
\(-0.3 x - 0.6 x^2 < 0\)
\(-0.3 x (1 + 2x) = 0\)
\(x_1 = 0, \quad x_2 = -\frac{1}{2}\)
Парабола направлена вниз, и решение уравнения это \(x \in (-\infty, -\frac{1}{2}) \cup (0, +\infty)\).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Решите неравенство: а) \(0,01x^{2}\leq 1\); б) \(\frac{1}{2}x^{2}>12\); в) \(4x\leq -x^{2}\) г) \(\frac{1}{3}x^{2}>\frac{1}{9}\); д) \(5x^{2}>2x\); е) \(-0,3x<0,6x^{2}\);
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
