§6. Неравенства с одной переменной — 16. Решение неравенств второй степени с одной переменной — 274 — стр. 91

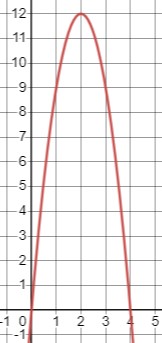
Рассмотрим функцию \(y=\sqrt{12 x-3}\).

Область определения определяется тем, что аргумент под корнем должен быть неотрицательным: \(12 x - 3 \geq 0\). Решая это неравенство, получаем \(x \geq \frac{1}{4}\).

Теперь найдем точки пересечения с осью \(Ox\) (где \(y=0\)). Уравнение \(3x(4-x)=0\) имеет корень \(x=0\), и интервал определения ограничен значением \(x=4\). Таким образом, область определения для функции \(y=\sqrt{12 x-3}\) - это интервал \([0, 4]\).

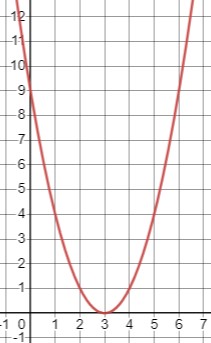
Рассмотрим функцию \(y=\frac{1}{\sqrt{2 x^{2}-12 x+18}}\).

Область определения определяется условием, что знаменатель не может быть равен нулю и должен быть положительным: \(2 x^{2}-12 x+18 > 0\). Решая это квадратное неравенство, получаем \((x-3)^2 > 0\), что эквивалентно \(x \neq 3\). Таким образом, область определения для этой функции - все значения \(x\), кроме \(x=3\).

Таким образом, область определения: \(x \in (-\infty, 3) \cup (3, +\infty)\).