Решите неравенство:
а) \((x+9)(x-2)(x-15)<0\);
б) \(x(x-5)(x+6)>0\);
в) \((x-1)(x-4)(x-8)(x-16)<0\).
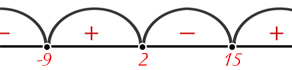
Рассмотрим уравнение \((x+9)(x-2)(x-15)\). Находим корни уравнения: \(x_{1}=-9\), \(x_{2}=2\), \(x_{3}=15\). Таким образом, решение представляет интервал:
\(x \in (-\infty, -9) \cup (2, 15)\).
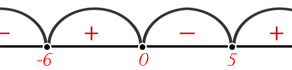
Решим неравенство \(x(x-5)(x+6)>0\). Находим корни уравнения: \(x_{1}=0\), \(x_{2}=5\), \(x_{3}=-6\). Таким образом, решение задачи:
\(x \in (-6, 0) \cup (5, +\infty)\).
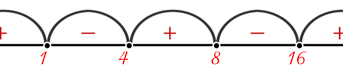
Рассмотрим неравенство \((x-1)(x-4)(x-8)(x-16)<0\). Находим корни уравнения: \(x_{1}=1\), \(x_{2}=4\), \(x_{3}=8\), \(x_{4}=16\). Таким образом, решение задачи:
\(x \in (1, 4) \cup (8, 16)\).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Решите неравенство: а) \((x+9)(x-2)(x-15)<0\); б) \(x(x-5)(x+6)>0\); в) \((x-1)(x-4)(x-8)(x-16)<0\).

