§6. Неравенства с одной переменной — Дополнительные упражнения к параграфу 5 — 319 — стр. 105

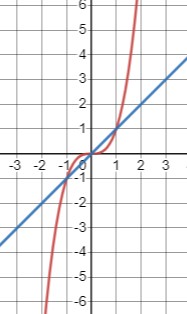
Рассмотрим уравнение \(y = x^{3}\) (красный график)
\(\frac{x}{y}|\frac{0}{0}|\frac{1}{2}|\frac{2}{8}\)
и \(y = x\) (синий график)
\(\frac{x}{y}\frac{0}{0}|\frac{1}{1}|\frac{2}{2}\)
Ищем точки их пересечения:
\(x^{3} = x\)
\(x^{3}-x = 0\)
\(x(x^{2} - 1) = 0\)
Таким образом, получаем три значения \(x\):
\(x_{1} = 0\)
\(x_{2,3} = \pm 1\)
Ответ: \(x_{1} = 0\), \(x_{2} = -1\), \(x_{3} = 1\).