§6. Неравенства с одной переменной — Дополнительные упражнения к параграфу 6 — 349 — стр. 108

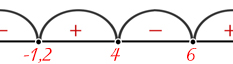
Рассмотрим неравенство \((x+1.2)(6-x)(x-4) > 0\).

Найдем корни уравнения, приравняв его нулю:

\((x+1.2)(6-x)(x-4) = 0.\)

Решение: \(x_1 = -1.2, x_2 = 6, x_3 = 4\).

Теперь используем метод интервалов. Выберем по одной точке из каждого интервала, образованного корнями.

1. Интервал \((-\infty, -1.2)\): Возьмем \(x = -2\).

2. Интервал \((-1.2, 4)\): Возьмем \(x = 0\).

3. Интервал \((4, 6)\): Возьмем \(x = 5\).

4. Интервал \((6, +\infty)\): Возьмем \(x = 7\).

Подставим эти значения в исходное неравенство, чтобы определить знак:

1. \((-2+1.2)(6+2)(-2-4) < 0\) - неравенство выполняется.

2. \((0+1.2)(6)(-4) < 0\) - неравенство выполняется.

3. \((5+1.2)(-1)(1) > 0\) - неравенство выполняется.

4. \((7+1.2)(2)(-6) < 0\) - неравенство выполняется.

Таким образом, решением исходного неравенства является \(x \in (-\infty, -1.2) \cup (4, 6)\).

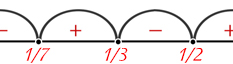
Рассмотрим неравенство \(\left(\frac{1}{3}-x\right)\left(\frac{1}{2}-x\right)\left(\frac{1}{2}-x\right) < 0\).

Найдем корни уравнения, приравняв его нулю:

\(\left(x-\frac{1}{3}\right)\left(x-\frac{1}{2}\right)\left(x-\frac{1}{7}\right) = 0.\)

Решение: \(x_1 = \frac{1}{7}, x_2 = \frac{1}{3}, x_3 = \frac{1}{2}\).

Теперь используем метод интервалов. Выберем по одной точке из каждого интервала, образованного корнями.

1. Интервал \(\left(-\infty, \frac{1}{7}\right)\): Возьмем \(x = 0\).

2. Интервал \(\left(\frac{1}{7}, \frac{1}{3}\right)\): Возьмем \(x = \frac{1}{4}\).

3. Интервал \(\left(\frac{1}{3}, \frac{1}{2}\right)\): Возьмем \(x = \frac{3}{8}\).

4. Интервал \(\left(\frac{1}{2}, +\infty\right)\): Возьмем \(x = 1\).

Подставим эти значения в исходное неравенство, чтобы определить знак:

1. \(\left(\frac{1}{3}-0\right)\left(\frac{1}{2}-0\right)\left(\frac{1}{2}-0\right) < 0\) - неравенство не выполняется.

2. \(\left(\frac{1}{3}-\frac{1}{4}\right)\left(\frac{1}{2}-\frac{1}{4}\right)\left(\frac{1}{2}-\frac{1}{7}\right) < 0\) - неравенство выполняется.

3. \(\left(\frac{1}{3}-\frac{3}{8}\right)\left(\frac{1}{2}-\frac{3}{8}\right)\left(\frac{1}{2}-\frac{3}{8}\right) < 0\) - неравенство выполняется.

4. \(\left(\frac{1}{3}-1\right)\left(\frac{1}{2}-1\right)\left(\frac{1}{2}-1\right) < 0\) - неравенство не выполняется.

Таким образом, решением исходного неравенства является \(x \in \left(\frac{1}{7}, \frac{1}{3}\right) \cup \left(\frac{1}{2}, +\infty\right)\).

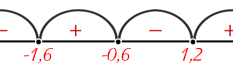
Рассмотрим неравенство \((x+0.6)(1.6+x)(1.2-x) > 0\).

Найдем корни уравнения, приравняв его нулю:

\((x+0.6)(x+1.6)(x-1.2) = 0.\)

Решение: \(x_1 = -0.6, x_2 = -1.6, x_3 = 1.2\).

Теперь используем метод интервалов. Выберем по одной точке из каждого интервала, образованного корнями.

1. Интервал \((- \infty, -1.6)\): Возьмем \(x = -2\).

2. Интервал \((-1.6, -0.6)\): Возьмем \(x = -1\).

3. Интервал \((-0.6, 1.2)\): Возьмем \(x = 0\).

4. Интервал \((1.2, +\infty)\):

Возьмем \(x = 2\).

Подставим эти значения в исходное неравенство, чтобы определить знак:

1. \((-2+0.6)(-0.4)(-3.2) > 0\) - неравенство выполняется.

2. \((-1+0.6)(0.6)(-2.2) > 0\) - неравенство выполняется.

3. \((0+0.6)(1.6)(2.4) > 0\) - неравенство выполняется.

4. \((2+0.6)(3.6)(-0.8) > 0\) - неравенство выполняется.

Таким образом, решением исходного неравенства является \(x \in (-\infty, -1.6) \cup (-0.6, 1.2)\).

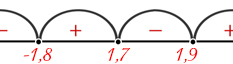
Рассмотрим неравенство \((1.7-x)(1.8+x)(1.9-x) < 0\).

Найдем корни уравнения, приравняв его нулю:

\((x-1.7)(x+1.8)(x-1.9) = 0.\)

Решение: \(x_1 = 1.7, x_2 = -1.8, x_3 = 1.9\).

Теперь используем метод интервалов. Выберем по одной точке из каждого интервала, образованного корнями.

1. Интервал \((- \infty, -1.8)\): Возьмем \(x = -2\).

2. Интервал \((-1.8, 1.7)\): Возьмем \(x = 0\).

3. Интервал \((1.7, 1.9)\): Возьмем \(x = 1.8\).

4. Интервал \((1.9, +\infty)\): Возьмем \(x = 2\).

Подставим эти значения в исходное неравенство, чтобы определить знак:

1. \((-2-1.7)(-0.2)(-3.9) < 0\) - неравенство выполняется.

2. \((0-1.7)(1.8)(-2.9) < 0\) - неравенство выполняется.

3. \((1.8-1.7)(3.6)(0.1) < 0\) - неравенство не выполняется.

4. \((2-1.7)(3.8)(0.1) < 0\) - неравенство выполняется.

Таким образом, решением исходного неравенства является \(x \in (-\infty, -1.8) \cup (1.7, 1.9)\).