§6. Неравенства с одной переменной — Дополнительные упражнения к параграфу 6 — 353 — стр. 108

Рассмотрим неравенство

\(\left(x^{2}+17\right)(x-6)(x+2)<0.\)

Для начала рассмотрим условие \(x^{2}+17>0\), которое выполняется для всех \(x\), так как квадрат любого числа не может быть отрицательным.

Теперь рассмотрим \((x-6)(x+2)<0\),

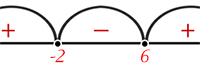
Точка пересечения равенств \(x-6=0\) и \(x+2=0\) это \(x_{1}=6\), \(x_{2}=-2\).

Применим метод интервалов:

\(x \in (-2, 6)\).

Рассмотрим неравенство

\(\left(2 x^{2}+1\right) x(x-4)>0.\)

Для начала рассмотрим условие \(2 x^{2}+1>0\), которое выполняется для любого \(x\), так как \(2 x^{2}\) всегда положительно.

Теперь рассмотрим \(x(x-4)>0\),

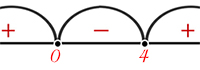
Точка пересечения равенств \(x=0\) и \(x-4=0\) это \(x_{1}=0,(x_{2}=4\).

Применим метод интервалов:

\(x \in (-\infty, 0) \cup (4, +\infty)\).

Рассмотрим неравенство

\((x-1)^{2}(x-24)<0.\)

Условие \((x-1)^{2} \geq 0\) выполняется для всех \(x\) (квадрат всегда неотрицателен), и при \(x=1\) достигается равенство.

Теперь рассмотрим \(x-24<0\),

Точка пересечения равенства \(x-24=0\) это \(x=24\).

Применим метод интервалов:

\(x \in (-\infty, 1) \cup (1, 24)\).

Рассмотрим неравенство

\((x+7)(x-4)^{2}(x-21)>0.\)

Условие \((x-4)^{2} \geq 0\) выполняется для всех \(x\), и при \(x=4\) достигается равенство.

Теперь рассмотрим \((x+7)(x-21)>0\),

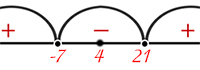
Точки пересечения равенств \(x+7=0\) и \(x-21=0\) это \(x_{1}=-7\) и \(x_{2}=21\).

Применим метод интервалов:

\(x \in (-\infty, -7) \cup (21, +\infty)\).