§6. Неравенства с одной переменной — Дополнительные упражнения к параграфу 6 — 354 — стр. 108

Рассмотрим уравнение

\(y=\frac{4}{\sqrt{(3 x-1)(6 x+1)}}.\)

Для начала рассмотрим условие \((3 x-1)(6 x+1)>0\),

Разложим выражение:

\(\left(x-\frac{1}{3}\right)\left(x+\frac{1}{6}\right)>0.\)

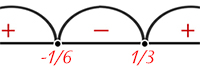
Точки пересечения с осью \(x\) равны \(x_1=\frac{1}{3}\) и \(x_2=-\frac{1}{6}\).

Применим метод интервалов:

\(x \in \left(-\infty, -\frac{1}{6}\right) \cup \left(\frac{1}{3}, +\infty\right)\).

Рассмотрим уравнение

\(y=\frac{7}{\sqrt{(11 x+2)(x-4)}}.\)

Для начала рассмотрим условие \((11 x+2)(x-4)>0\),

Разложим выражение:

\(\left(x+\frac{2}{11}\right)\left(x-4\right)>0.\)

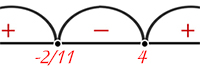
Точки пересечения с осью \(x\) равны \(x_1=-\frac{2}{11}\) и \(x_2=4\).

Применим метод интервалов:

\(x \in \left(-\infty, -\frac{2}{11}\right) \cup (4, +\infty)\).