§7. Уравнения с двумя перемннными и их системы — 19. Уравнение с двумя переменными и его график — 377 — стр. 116

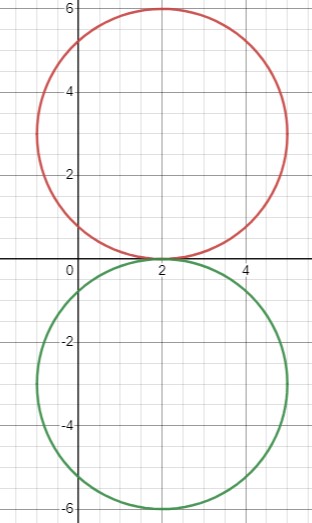
Симметрия относительно оси абсцисс \(x \rightarrow x, y \rightarrow -y\). Таким образом, образ центра \((2, -3)\) относительно оси абсцисс будет \((2, 3)\), и уравнение окружности примет вид \((x-2)^{2}+(y-3)^{2}=9\).

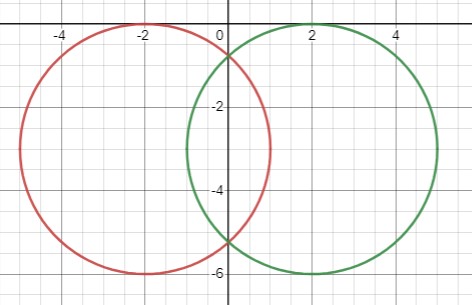
Симметрия относительно оси ординат \(x \rightarrow -x, y \rightarrow y\). Образ центра \((2, -3)\) относительно оси ординат будет \((-2, -3)\), уравнение окружности примет вид \((x+2)^{2}+(y+3)^{2}=9\).

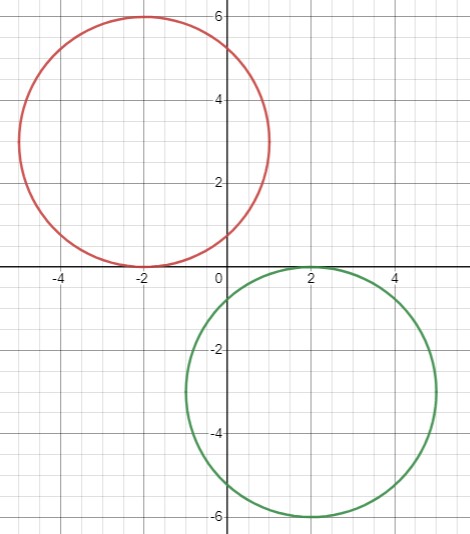
Симметрия относительно начала координат \(x \rightarrow -x, y \rightarrow -y\). Образ центра \((2, -3)\) относительно начала координат будет \((-2, 3)\), уравнение окружности примет вид \((x+2)^{2}+(y-3)^{2}=9\).