Физика
2024
Две концентрические окружности, заданные уравнениями \(x^{2}+y^{2}=9\) и \(x^{2}+y^{2}=16\), делят плоскость на три области: кольцо, ограниченное окружностями, часть плоскости, ограниченную малой окружностью, и часть плоскости, находящуюся за пределами круга, ограниченного большой окружностью. В какой из трёх областей расположены точки: \(M(5; 5)\), \(N(1;-2)\), \(P(3,6; 0)\), \(Q(4,001;-0,5)\)? Сделайте схематический рисунок.
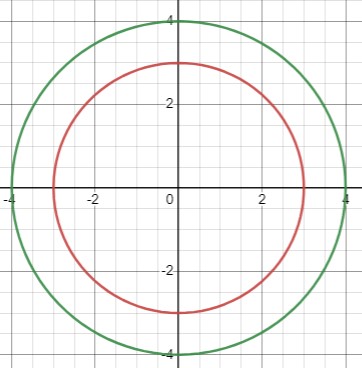
Точки \(M\) и \(Q\) находятся за пределами большой окружности:
\(\sqrt{5^2 + 5^2} > 4 \quad \text{и} \quad \sqrt{4.001^2 + (-0.5)^2} > 4\)
Теперь рассмотрим точку \(P\) и проверим, находится ли она в кольце между окружностями:
\(3 < \sqrt{3.6^2 + 0^2} < 4\)
Наконец, проверим, что точка \(N\) расположена внутри малой окружности.
\(\sqrt{1^2 + (-2)^2} = \sqrt{5} <3\).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Две концентрические окружности, заданные уравнениями \(x^{2}+y^{2}=9\) и \(x^{2}+y^{2}=16\), делят плоскость на три области: кольцо, ограниченное окружностями, часть плоскости, ограниченную малой окружностью, и часть плоскости, находящуюся за пределами круга, ограниченного большой окружностью. В какой из трёх областей расположены точки: \(M(5; 5)\), \(N(1;-2)\), \(P(3,6; 0)\), \(Q(4,001;-0,5)\)? Сделайте схематический рисунок.
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
