§8. Неравенства с двумя переменными и их системы — 23. Неравенства с двумя переменными — 458 — стр. 134

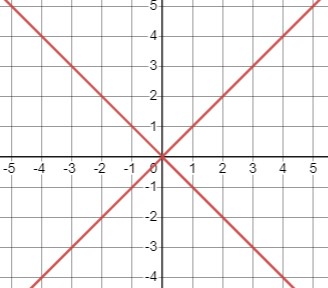
Уравнение \(x^2 - y^2 = 0\) можно представить в виде разности квадратов: \((x-y)(x+y) = 0\). Отсюда получаем два уравнения: \(x-y = 0\) и \(x+y = 0\). Решая первое уравнение, получаем \(y = x\), а решая второе, получаем \(y = -x\). Таким образом, у нас есть две линии, представленные уравнением \(x^2 - y^2 = 0\): \(y = x\) и \(y = -x\).

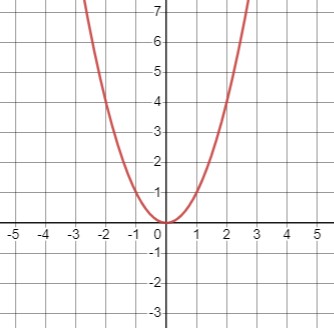
Рассмотрим уравнение \(\frac{x^2 - y}{x} = 0\). Определение функции требует, чтобы знаменатель не был равен нулю, поэтому областью определения является \(x \neq 0\). Решая уравнение \(x^2 - y = 0\), получаем \(y = x^2\).

Таким образом, уравнение представляет собой параболу с ветвями, открытыми вверх.