(Для работы в парах.) Покажите штриховкой на координатной плоскости множество решений системы неравенств:
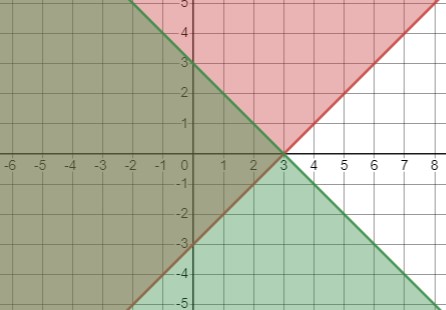
a) \(\left\{\begin{array}{l}y \geq x-3 \\y \leq -x+3\end{array}\right.\)
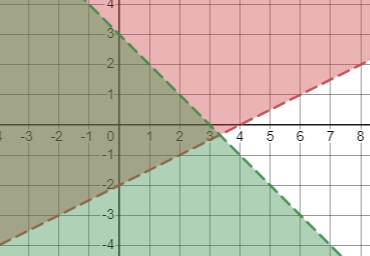
б) \(\left\{\begin{array}{l}x-2y<4 \\x+y<3\end{array}\right.\)
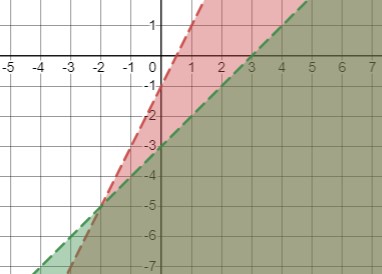
в) \(\left\{\begin{array}{l}-2x+y<-1 \\ x-y>3\end{array}\right.\)
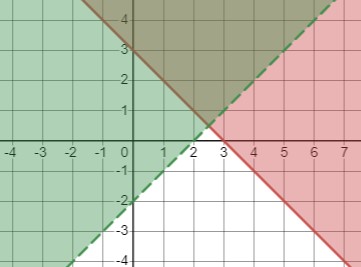
г) \(\left\{\begin{array}{l}x+y \geq 3 \\x-y<2\end{array}\right.\)
1) Обсудите, к какому виду удобно привести неравенства системы в заданиях б), в) и г).
2) Распределите, кто выполняет задания а) и в), а кто - задания б) и г), и выполните их.
3) Проверьте друг у друга, правильно ли показано множество решений системы неравенств в каждом случае.
а
\(\begin{cases} y \geq x - 3 \\ y \leq -x + 3 \end{cases}\)
б
\(\begin{cases} x - 2y < 4 \\ x + y < 3 \end{cases}\)
в
\(\begin{cases} -2x + y < -1 \\ x - y > 3 \end{cases}\)
г
\(\begin{cases} x + y \geq 3 \\ x - y < 2 \end{cases}\)
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
(Для работы в парах.) Покажите штриховкой на координатной плоскости множество решений системы неравенств: a) \(\left\{\begin{array}{l}y \geq x-3 \\y \leq -x+3\end{array}\right.\) б) \(\left\{\begin{array}{l}x-2y<4 \\x+y<3\end{array}\right.\) в) \(\left\{\begin{array}{l}-2x+y<-1 \\ x-y>3\end{array}\right.\) г) \(\left\{\begin{array}{l}x+y \geq 3 \\x-y<2\end{array}\right.\) 1) Обсудите, к какому виду удобно привести неравенства системы в заданиях б), в) и г). 2) Распределите, кто выполняет задания а) и в), а кто - задания б) и г), и выполните их. 3) Проверьте друг у друга, правильно ли показано множество решений системы неравенств в каждом случае.
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
