Изобразите на координатной плоскости множество решений системы:
a) \(\left\{\begin{array}{l}y \geq x^{2} \\y \leq 4\end{array}\right.\)
б) \(\left\{\begin{array}{l}x^{2}+y^{2} \leq 4, \\x-y \geq 0\end{array}\right.\)
в) \(\left\{\begin{array}{l}x^{2}+y^{2} \leq 9 \\(x-3)^{2}+y^{2} \leq 9\end{array}\right.\)
г) \(\left\{\begin{array}{l}(x-2)^{2}+(y+1)^{2} \geq 1, \\(x-2)^{2}+(y+1)^{2} \leq 9\end{array}\right.\)
а
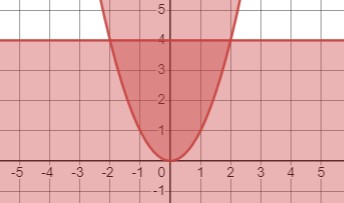
Рассмотрим систему неравенств:
\(\begin{cases} y \geq x^{2} \\ y \leq 4 \end{cases}\)
Первое неравенство задает множество точек, расположенных выше графика функции \(y=x^{2}\), включая точки, принадлежащие графику. Второе неравенство определяет множество точек, расположенных ниже графика функции \(y=4\), включая точки, принадлежащие графику.
б
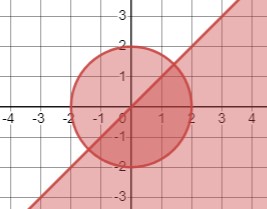
Рассмотрим систему неравенств:
\(\begin{cases} x^{2}+y^{2} \leq 4 \\ x-y \geq 0 \end{cases}\)
Преобразуем неравенства:
\(\begin{cases} x-y \geq 1 \\ x^{2}+y^{2} \leq 4 \end{cases}\)
Первое неравенство задает множество точек, расположенных ниже графика функции \(y=x-1\), включая сам график. Второе неравенство определяет множество точек, расположенных внутри окружности с центром в начале координат и радиусом 2, включая точки, принадлежащие окружности.
в
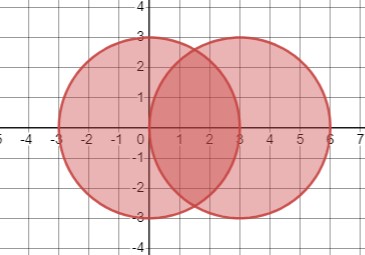
\(\left\{\begin{array}{c}x^2+y^2 \leq 9 \\(x-3)^2+y^2 \leq 9\end{array}\right.\)
Первое неравенство описывает множество точек, которые находятся внутри окружности с центром в начале координат и радиусом 3, включая точки, лежащие на самой окружности. Второе неравенство определяет множество точек, которые находятся внутри окружности с центром в точке (3, 0) и радиусом также равным 3, включая точки, принадлежащие этой окружности.
г
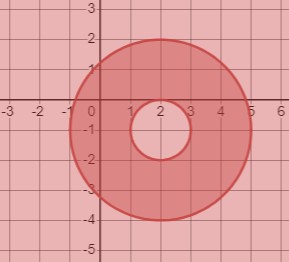
Рассмотрим систему неравенств:
\(\begin{cases} (x-2)^{2}+(y+1)^{2} \geq 1 \\ (x-2)^{2}+(y+1)^{2} \leq 9 \end{cases}\)
Первое неравенство задает множество точек, расположенных вне окружности с центром в точке \((2 ;-1)\) и радиусом 1, включая точки, принадлежащие границе окружности. Второе неравенство определяет множество точек, расположенных внутри окружности с центром в точке \((2 ;-1)\) и радиусом 3, включая точки, принадлежащие границе окружности.
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Изобразите на координатной плоскости множество решений системы: a) \(\left\{\begin{array}{l}y \geq x^{2} \\y \leq 4\end{array}\right.\) б) \(\left\{\begin{array}{l}x^{2}+y^{2} \leq 4, \\x-y \geq 0\end{array}\right.\) в) \(\left\{\begin{array}{l}x^{2}+y^{2} \leq 9 \\(x-3)^{2}+y^{2} \leq 9\end{array}\right.\) г) \(\left\{\begin{array}{l}(x-2)^{2}+(y+1)^{2} \geq 1, \\(x-2)^{2}+(y+1)^{2} \leq 9\end{array}\right.\)
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
