Обществознание
2023
Решите графически систему уравнений:
а) \(\left\{\begin{array}{l}y+x+x^{2}=0 \\x-y=10\end{array}\right.\)
б) \(\left\{\begin{array}{l}(x-2)^{2}+y^{2}=9 \\y=x^{2}-4x+4\end{array}\right.\)
в) \(\left\{\begin{array}{l}x^{2}+y^{2}=25, \\y=2x^{2}-14\end{array}\right.\)
г) \(\left\{\begin{array}{l}x^{2}+y^{2}=10, \\xy=3\end{array}\right.\)
д) \(\left\{\begin{array}{l}x+y=8, \\(x+1)^{2}+y^{2}=81\end{array}\right.\)
e) \(\left\{\begin{array}{l}y=-x^{2}+4, \\y=|x|\end{array}\right.\)
а
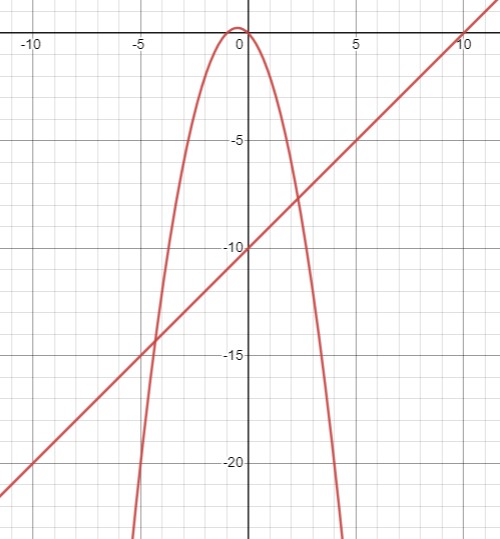
\(\begin{cases}y + x + x^2 = 0 \\x - y = 10\end{cases} \)
\(\begin{cases}y = -x - x^2 \\y = x - 10\end{cases} \)
Ответ: (-4,2 ;-14,2), (2,2 ;-7,7).
б
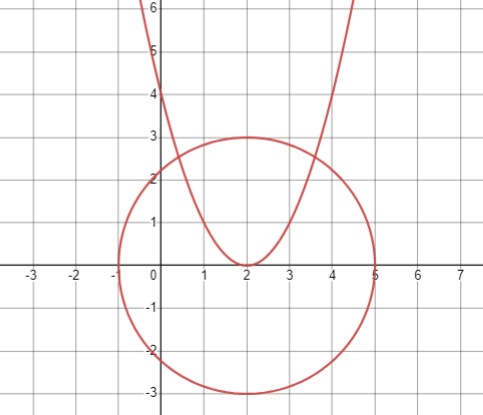
\(\begin{cases}(x - 2)^2 + y^2 = 9 \\y = x^2 - 4x + 4\end{cases}\)
\(\begin{cases}(x - 2)^2 + y^2 = 9 \\y = (x - 2)^2\end{cases}\)
\((x - 2)^2 + y^2 = 9 \text{ (окружность, центр (2, 0), радиус 3)}\)
Ответ: (0,4; 2,5), (3,6; 2,5).
в
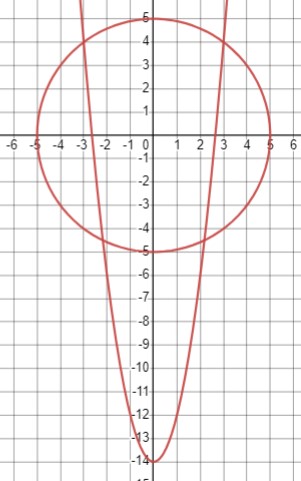
\(\begin{cases}x^2 + y^2 = 25 \\y = 2x^2 - 14\end{cases}\)
\(x^2 + y^2 = 25 \text{ (окружность, синий график, центр (0, 0), радиус 5)}\)
Ответ: (-3 ; 4), (-2,2 ;-4,5), (2,2 ;-4,5), (3 ; 4).
г
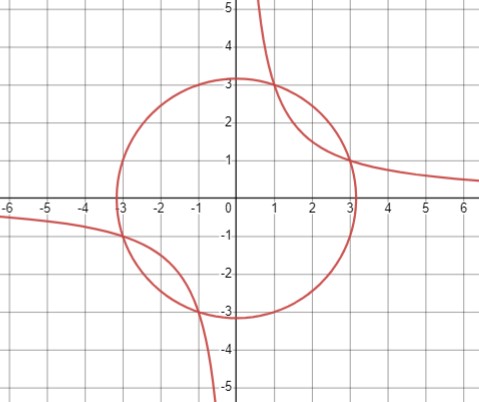
\(\begin{cases}x^2 + y^2 = 10\\xy=3\end{cases}\)
\(x^2 + y^2 = 10\) - окружность с центром в начале координат и радиусом \(\sqrt{10})\)
Ответ: (-3 ;-1), (-1 ;-3), (1 ; 3), (3 ; 1).
д
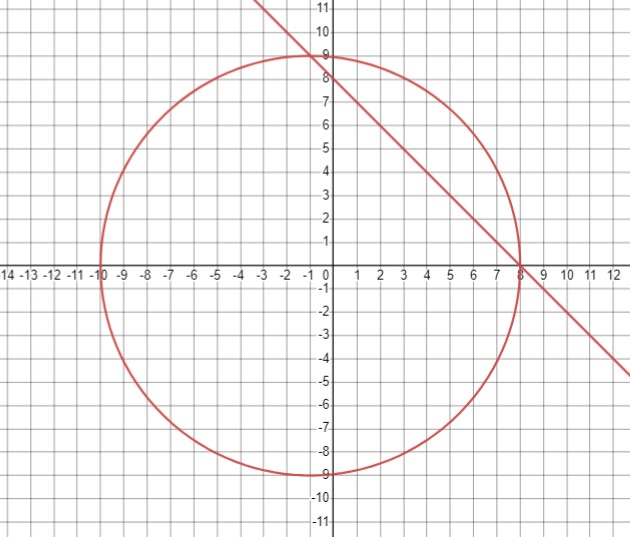
\(\begin{cases}x + y = 8 \\(x + 1)^2 + y^2 = 81\end{cases} \)
\((x + 1)^2 + y^2 = 81 \text { (окружность с центром в точке } (-1, 0) \text { и радиусом 9)}\)
Ответ: (-1 ; 9), (8 ; 0).
е
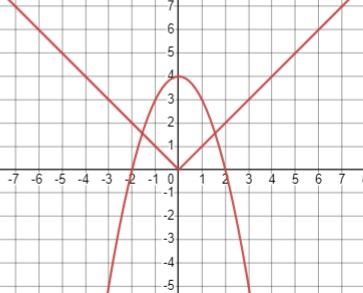
\(\begin{cases}y = -x^2 + 4 \\y = |x|\end{cases} \)
Ответ: (-1,6 ; 1,6), (1,6 ; 1,6).
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Решите графически систему уравнений: а) \(\left\{\begin{array}{l}y+x+x^{2}=0 \\x-y=10\end{array}\right.\) б) \(\left\{\begin{array}{l}(x-2)^{2}+y^{2}=9 \\y=x^{2}-4x+4\end{array}\right.\) в) \(\left\{\begin{array}{l}x^{2}+y^{2}=25, \\y=2x^{2}-14\end{array}\right.\) г) \(\left\{\begin{array}{l}x^{2}+y^{2}=10, \\xy=3\end{array}\right.\) д) \(\left\{\begin{array}{l}x+y=8, \\(x+1)^{2}+y^{2}=81\end{array}\right.\) e) \(\left\{\begin{array}{l}y=-x^{2}+4, \\y=|x|\end{array}\right.\)
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
