Rainbow English
2018
Изобразив схематически графики уравнений, определите, имеет ли решения система уравнений и сколько:
а) \(\left\{\begin{array}{l}x^{2}-y+11=0, \\y+x^{2}=4\end{array}\right.\)
б) \(\left\{\begin{array}{l}(x+3)^{2}+(y+4)^{2}=1 \\(x-2)^{2}+(y-1)^{2}=4\end{array}\right.\)
в) \(\left\{\begin{array}{l}y=|x|, \\\frac{1}{2}x^{3}-y=0\end{array}\right.\)
а
Рассмотрим систему уравнений:
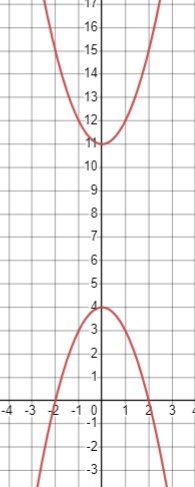
\(\left\{\begin{array}{c}x^2 - y + 11 = 0 \\y + x^2 = 4\end{array}\right.\)
Перепишем второе уравнение в виде \(y = 4 - x^2\). Теперь мы имеем систему:
\(\left\{\begin{array}{c}y = x^2 + 11 \\y = 4 - x^2\end{array}\right.\)
На графике видно, что графики не пересекаются. Следовательно, система уравнений не имеет решений.
б
Изучим систему уравнений:
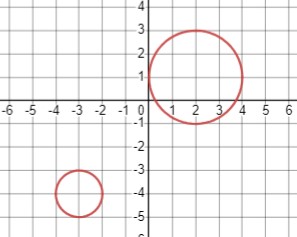
\(\left\{\begin{array}{l}(x + 3)^2 + (y + 4)^2 = 1 \\(x - 2)^2 + (y - 1)^2 = 4\end{array}\right.\)
Первое уравнение описывает окружность с центром в точке \((-3, -4)\) и радиусом 1, а второе уравнение - окружность с центром в точке \((2, 1)\) и радиусом 2.
Графики этих окружностей не пересекаются, следовательно, система уравнений не имеет решений.
в
Исследуем систему уравнений:
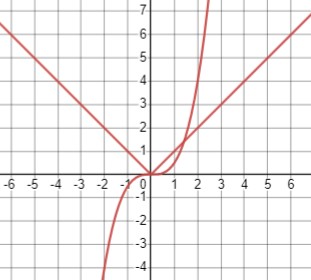
\(\left\{\begin{array}{c}y = |x| \\\frac{1}{2} x^3 - y = 0\end{array}\right.\)
Графики пересекаются в двух точках: \((-1, -\frac{1}{2})\) и \((1, \frac{1}{2})\). Следовательно, система имеет два решения.
Решебник
"Алгебра - Учебник" по предмету Математика за 9 класс.
Aвторы:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Задание
Изобразив схематически графики уравнений, определите, имеет ли решения система уравнений и сколько: а) \(\left\{\begin{array}{l}x^{2}-y+11=0, \\y+x^{2}=4\end{array}\right.\) б) \(\left\{\begin{array}{l}(x+3)^{2}+(y+4)^{2}=1 \\(x-2)^{2}+(y-1)^{2}=4\end{array}\right.\) в) \(\left\{\begin{array}{l}y=|x|, \\\frac{1}{2}x^{3}-y=0\end{array}\right.\)
Еще решебники за 9 класс
Мы подобрали сборники ГДЗ за 9 класс, которые могут быть Вам интересны.
